https://sh1mj1-log.tistory.com/140 이전 글에서 계속 됩니다.
백준 1707 이분 그래프
https://www.acmicpc.net/problem/1707
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
1. 문제 분석

노드를 집합 2개로 나눌 때 인접한 노드끼리 같은 집합이 되면 안 됩니다. 즉, 같은 위 그림처럼 인접해있으면 색이 달라야 한다는 의미입니다. 만약 사이클이 발생한다면 이분 그래프가 불가능합니다.
이런 경우를 어떻게 알아낼 수 있을까요? 탐색 매커니즘에서 탐색한 노드에 다시 접근하게 되었을 때 현재 노드의 집합(색깔)과 같으면 이분 그래프가 불가능하다 라고 알 수 있습니다.
2. 손으로 풀기

위 과정으로 해결하면 됩니다.
1. 그래프와 방문 배열, 집합 배열을 초기화.
2. 방문하지 않은 배열에 대해서 DFS 탐색 실행. 인접 노드에 대해서 집합배열값을 (현재 노드의 집합배열값 +1) % 2 의 값으로 넣기
만약 현재 노드의 집합배열값이 0 이었다면 인접 노드들의 집합배열값은 1 이 되고, 현재 노드의 집합 배열값이 1 이었다면 인접 노드들의 집합배열값은 0이 된다.
3. 2번의 과정을 진행하면서 만약 인접 노드 중 방문한 노드 X 가 있을 때 X 의 집합 배열값이 현재 노드의 집합 배열값과 같은 경우, 이분 그래프가 불가능한 것이다. 그러므로 이 데이터를 boolean 값으로 저장해두고 리턴. 결과 출력
3. 슈도코드
T: 테스트 케이스
graph: 인접 리스트, biSetArr: 이분 집합 배열
visited: 방문 배열
isBipartite = true: 이분인지?
for(T){
V: 노드 개수, E: 에지개수
for(V){ graph 초기화 }
for(E){ 에지 정보 추가 }
for(1 ~ V){
만약 방문하지 않았고 아직 이분 그래프로 보이면
dfsFunc(i)
}
if(isBiportite){ YES 출력 } 아니면 {NO 출력}
}
// dfs 메소드
dfsFunc(int node){
visited[node] = true;
for(int adjNode: 현재 노드의 인접 노드){
if(인접 노드가 방문한 노드라면){
if(biSetArr[인접노드] == biSetArr[node]){ // 현재 노드와 인접노드가 같은 집합이다?
isBipartite = false;
return;
}
} 아니라면{
biSetArr[인접노드] = (biSetArr[현재 노드] + 1) % 2 // 0 과 1 왔다갔다.
dfsFunc(adjNode)
}
}
}4. 코드
public class BaekJun1707 {
static BufferedReader br;
static ArrayList<Integer>[] graph;
static int[] biSetArr;
static boolean[] visited;
static boolean isBipartite;
public static void main(String[] args) throws IOException {
testCase();
}
private static void testCase() throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
for (int t = 0; t < T; t++) {
input();
}
}
private static void input() throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
graph = new ArrayList[V + 1];
biSetArr = new int[V + 1];
visited = new boolean[V + 1];
isBipartite = true;
for (int i = 1; i <= V; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int sta = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph[sta].add(end);
graph[end].add(sta);
}
for (int i = 1; i <= V; i++) {
if (!visited[i] && isBipartite) {
dfsFunc(i);
}
}
if (isBipartite) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
static void dfsFunc(int node) {
visited[node] = true;
for (int adjNode : graph[node]) {
if (visited[adjNode]) {
if (biSetArr[adjNode] == biSetArr[node]) {
isBipartite = false;
return;
}
} else {
biSetArr[adjNode] = (biSetArr[node] + 1) % 2;
dfsFunc(adjNode);
}
}
}
}
백준 2251 물통
https://www.acmicpc.net/problem/2251\
2251번: 물통
각각 부피가 A, B, C(1≤A, B, C≤200) 리터인 세 개의 물통이 있다. 처음에는 앞의 두 물통은 비어 있고, 세 번째 물통은 가득(C 리터) 차 있다. 이제 어떤 물통에 들어있는 물을 다른 물통으로 쏟아 부
www.acmicpc.net
1. 문제분석
그래프 데이터를 저장하고 저장한 자료구조를 이용하는 방식과 달리 그래프 원리를 적용해서 그래프를 역으로 그리는 방식으로 접근하는 문제입니다.
물통 A, B, C 의 특정 무게 상태를 1개의 노드로 가정하고 조건에 따라 이 상태에서 변경할 수 있는 무게 상태가 에지로 이어진 인접한 노드라고생각하고 문제에 접근합니다.
2. 손으로 풀기
위에서 물통 A, B, C 의 특정 무게 상태를 1개의 노드로 한다고 했습니다. 그런데 두 개의 상태만 알면 나머지 하나는 자동으로 정해집니다. 따라서 노드는 물통 A와 B 의 물의 양을 가진다고 하겠습니다. (손으로 풀 때는 눈으로 보기 편하게 하기 위해 노드를 A, B, C 의 값을 가진다고 하고 풀겠습니다.)
1. 처음에는 물통 A, B 는 비어있고 C 는 꽉차 있으므로 최초 출발 노드를 (0, 0, 3번째 물통의 용량) 으로 초기화 합니다.
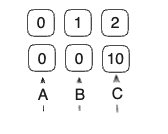
2. BFS 을 수행합니다. 탐색 과정을 아래와 같습니다.
a. 노드에서 갈 수 있는 6개의 경우(A -> B, A -> C, B -> A, B -> C, C -> A, C -> B) 에 관해서 다음 노드로 정해 큐에 추가합니다. 이 때 만약 A, B, C 무게가 동일한 노드에 방문한 이력이 있을 때는 큐에 추가하지 않습니다.
b. 보내는 물통의 모든 용량을 받는 물통에 저장하고 보내는 물통에는 0 을 저장합니다. 단, 받는 물통이 넘칠 때는 초과하는 값만큼 보내는 물통에 남깁니다.
c. 큐에 추가하는 시점에 1번째 물통 A 의 무게가 0일 때가 있으면 3번째 물통 C 의 값을 정답 배열에 추가합니다.

위 그림과 같은 방법으로 BFS 을 실행하면 될 것으로 보입니다.
이렇게 각 노드(A, B, C 물의 상태) 을 방문할 때마다 A의 물통이 비어있으면 C 물통에 있는 물의 양을 저장한 후에 이를 오른차순으로 정렬한 뒤 출력하면 됩니다.
3. 슈도 코드
SndrIndex, RcvrIndex: 6사지 경우를 탐색하기 위한 선언 배열
answer: 정답 배열
now: A, B, C 의 값을 저장하는 배열
now 배열 저장.
visited, answer 초기화
BFS 수행
for(answer 배열){
answer 배열에서 값이 true 인 index 을 정답으로 출력
}
// BFS 메서드
BFS {
큐 자료구조에 출발 노드 더하기 -> A, B 가 0 인 상태이므로 0,0 노드에서 시작.
visited 배열에 현재 노드 방문 기록.
answer 배열에 현재 C 의 값 체크
while(큐가 빌때까지){
큐에서 노드 데이터를 poll
A, B, C 값 초기화
for(6 가지 케이스 반복 ) { // A->B, A->C, B->A, B->C, C->A, C->B
받는 물통에 보내려는 물통의 값을 더하기
보내려는 물통 값을 0으로 업데이트
if(받는 물통이 넘치면){
넘치는 만큼 보내는 물통에 다시 넣어주고, 받는 물통은 이 물통의 최대값으로 저장
}
현재 노드의 연결 노드 중 방문하지 않은 노드로 큐에 add
visited 배열에 방문 기록
if(1번째 물통이 비어있으면) { 3번째 물통의 물의 양을 answer 배열에 기록하기 }
}
}
}
// ABbottle 클래스 선언.
// A, B 의 값만 가니고 있으면 C 는 구할 수 있다.
class ABbottle{
A, B
}
4. 코드
public class BaekJun2251 {
static int[] sndrIndex = {0, 0, 1, 1, 2, 2};
static int[] rcvrIndex = {1, 2, 0, 2, 0, 1};
static boolean[][] visited;
static int[] capacity;
static boolean[] answer;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
capacity = new int[3];
visited = new boolean[201][201];
answer = new boolean[201];
capacity[0] = Integer.parseInt(st.nextToken());
capacity[1] = Integer.parseInt(st.nextToken());
capacity[2] = Integer.parseInt(st.nextToken());
bfsFunc();
for (int i = 0; i < answer.length; i++) {
if (answer[i]) {
System.out.print(i + " ");
}
}
}
static void bfsFunc() {
Queue<ABbottle> qu = new LinkedList<>();
qu.add(new ABbottle(0, 0));
visited[0][0] = true;
answer[capacity[2]] = true;
while (!qu.isEmpty()) {
ABbottle cur = qu.poll();
int A = cur.A;
int B = cur.B;
int C = capacity[2] - A - B;
for (int i = 0; i < 6; i++) {
int[] next = {A, B, C};
next[rcvrIndex[i]] += next[sndrIndex[i]];
next[sndrIndex[i]] = 0;
if (next[rcvrIndex[i]] > capacity[rcvrIndex[i]]) {
int diff = next[rcvrIndex[i]] - capacity[rcvrIndex[i]];
next[rcvrIndex[i]] = capacity[rcvrIndex[i]];
next[sndrIndex[i]] = diff;
}
if (!visited[next[0]][next[1]]) {
qu.offer(new ABbottle(next[0], next[1]));
visited[next[0]][next[1]] = true;
if (next[0] == 0) {
answer[next[2]] = true;
}
}
}
}
}
static class ABbottle {
int A;
int B;
public ABbottle(int a, int b) {
A = a;
B = b;
}
}
}
'Java > 코딩테스트' 카테고리의 다른 글
| 위상정렬 자바 백준 BOJ 2252, 1516, 1948 (0) | 2023.08.07 |
|---|---|
| 유니온 파인드 자바 백준 BOJ 1717, 1976, 1043 (0) | 2023.08.05 |
| 그래프 표현-1 자바 백준 BOJ 18352, 1325 (0) | 2023.07.28 |
| 확장 유클리드 호제법 자바 백준 BOJ 21568 Ax+By=C (0) | 2023.07.26 |
| 유클리드 호제법 -2 자바 백준 BOJ 1033 칵테일 (0) | 2023.07.26 |