트리(Tree) 는 노드와 에지로 연결된 그래프의 특수한 형태입니다.
- 순한 구조(cycle) 이 없고, 1개의 루트 노드가 존재.
- 루트 노드를 제외한 노드는 단, 1개의 부모 노드를 가짐.
- 트리의 부분 트리(subtree) 역시 트리의 모든 특징을 따름.

리프노드는 트리에서 가장 하위에 존재하는 노드(자식 노드가 없는 노드) 입니다.
백준 11725 트리의 부모 찾기
https://www.acmicpc.net/problem/11725
11725번: 트리의 부모 찾기
루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.
www.acmicpc.net
1. 문제 분석
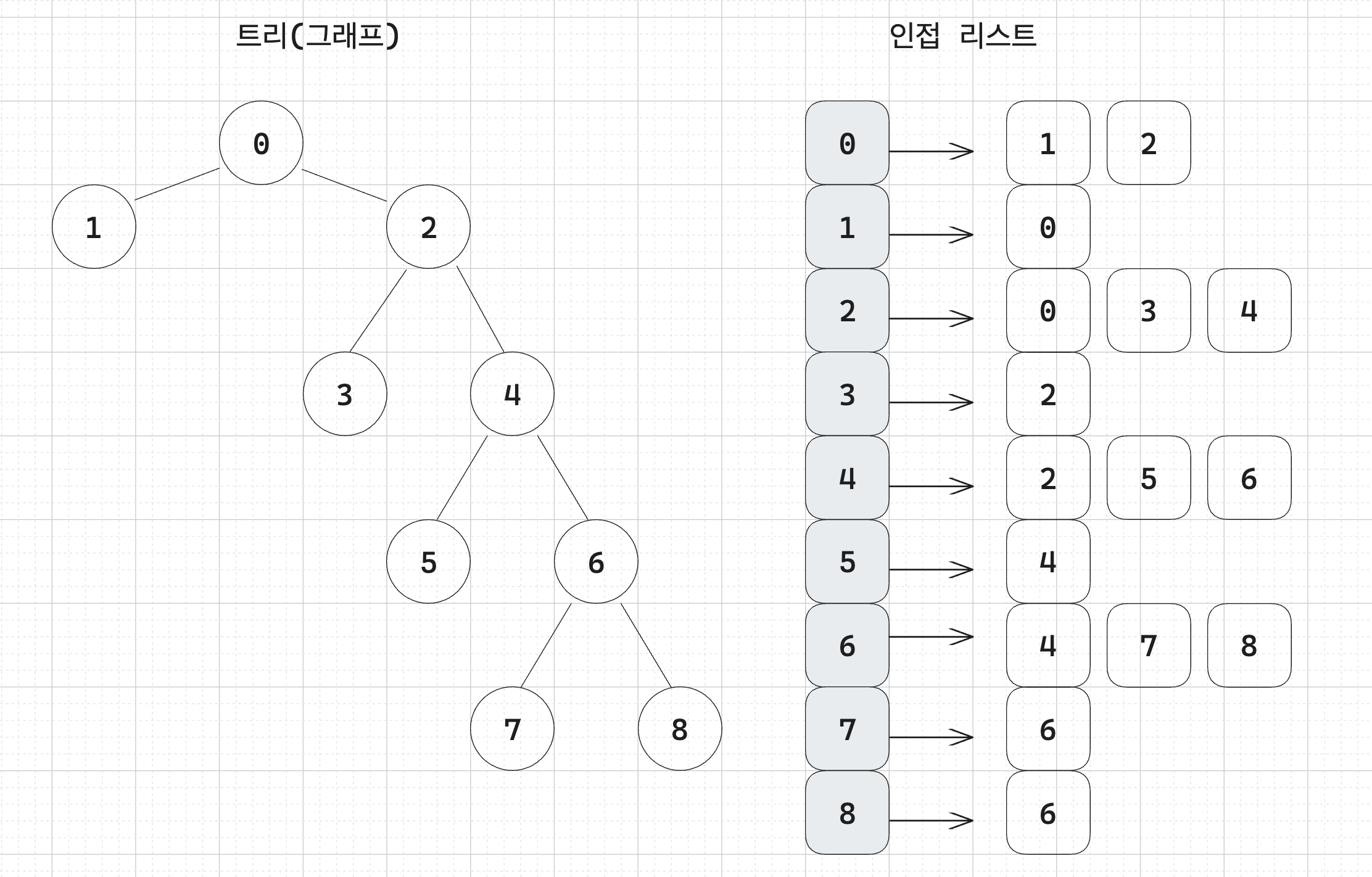
주어지는 데이터가 단순히 연결되어 있는 두 노드를 알려 주는 것이므로 데이터 저장 시 양방향 에지로 저장합니다. 트리(그래프)를 인접리스트 자료구조로 저장하면 편하게 데이터를 저장할 수 있습니다.
트리의 루트가 1 이므로 1번 노드부터 DFS 로 탐색하여 부모 노드를 찾아주면 문제를 쉽게 해결할 수 있습니다.
2. 손으로 풀기
a. 인접 리스트로 트리 데이터를 구현.
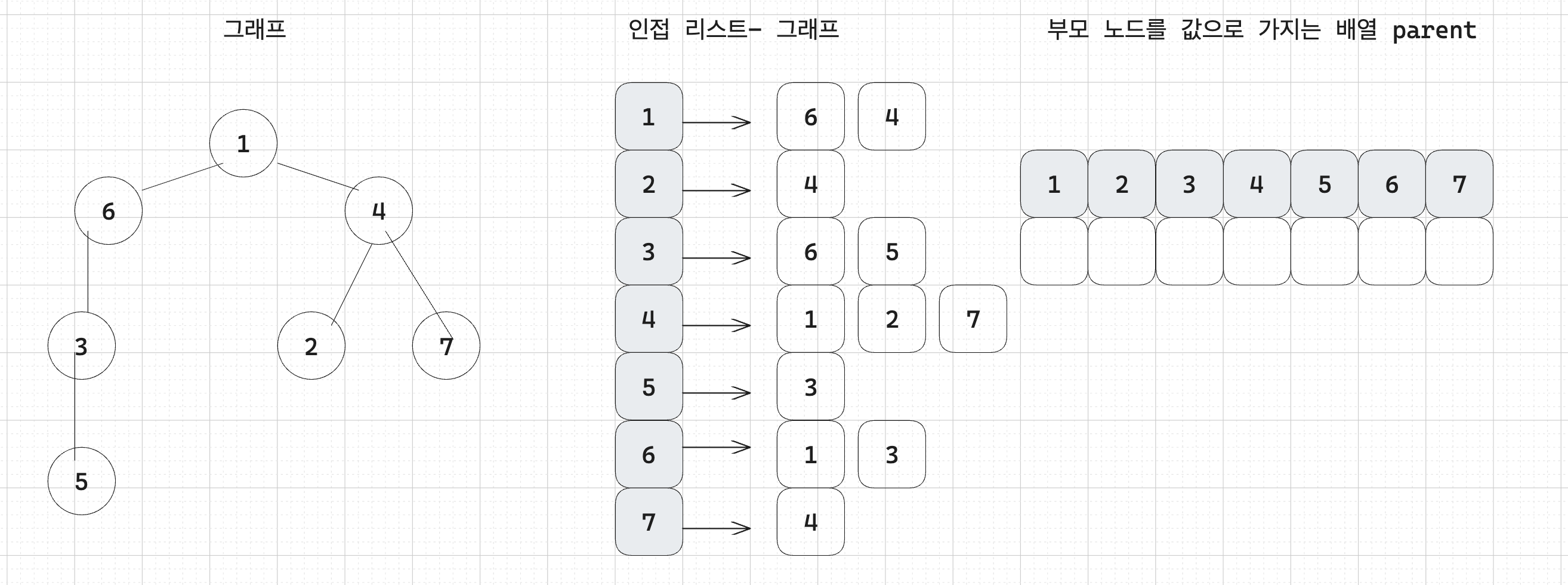
b. DFS 탐색을 수행하면서 부모 노드의 값을 parent 배열에 저장.

c. 정답 배열의 2번 인덱스부터 값을 차례대로 출력.
3. 슈도코드
N: 노드 개수
graph: 인접 리스트 ArrayList<Integer>[]
graph 에 데이터 입력 받기
parent: 각 노드으 ㅣ부모 노드를 저장하는 배열
visited: 방문 배열
DFS(1)
parent 의 데이터를 인덱스 2부터 값 출력
// DFS 함수
DFS(int node){
for(현재 node 와 인접 노드 next 들에 대해서){
방문한 적이 없다면
parent[next] = node;
DFS(node)
}
}
4. 코드
public class BaekJun11725 {
static ArrayList<Integer>[] graph;
static int[] parent;
static boolean[] visited;
static int N;
public static void main(String[] args) throws IOException {
input();
dfsFunc(1);
output();
}
private static void input() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
graph = new ArrayList[N + 1];
parent = new int[N+1];
visited = new boolean[N+1];
for (int i = 1; i <= N; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < N - 1; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph[start].add(end);
graph[end].add(start);
}
}
static void dfsFunc(int node) {
visited[node] = true;
for (int nextNode : graph[node]) {
if (!visited[nextNode]) {
parent[nextNode] = node;
dfsFunc(nextNode);
}
}
}
private static void output() {
for (int i = 2; i <= N; i++) {
System.out.println(parent[i]);
}
}
}
백준 1068 트리
https://www.acmicpc.net/problem/1068
1068번: 트리
첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다
www.acmicpc.net
1. 문제 분석
트리를 구성한 후 리프노드 개수를 세거 삭제할 노드에서부터 DFS 탐색을 하여 리프 노드 개수를 다시 셉니다. 그리고 그 두 개수에 대해 뺄셈 연산을 하면 정답을 구할 수 있을 것 같습니다.
2. 손으로 풀기
a. 먼저 그래프를 인접 리스트로 저장. 각 노드의 부모 노드를 저장하고 처음 상태에서의 리프노드의 개수(leafCnt)를 구한다.
처음 상태에서는 리프노드의 개수가 5개이다.
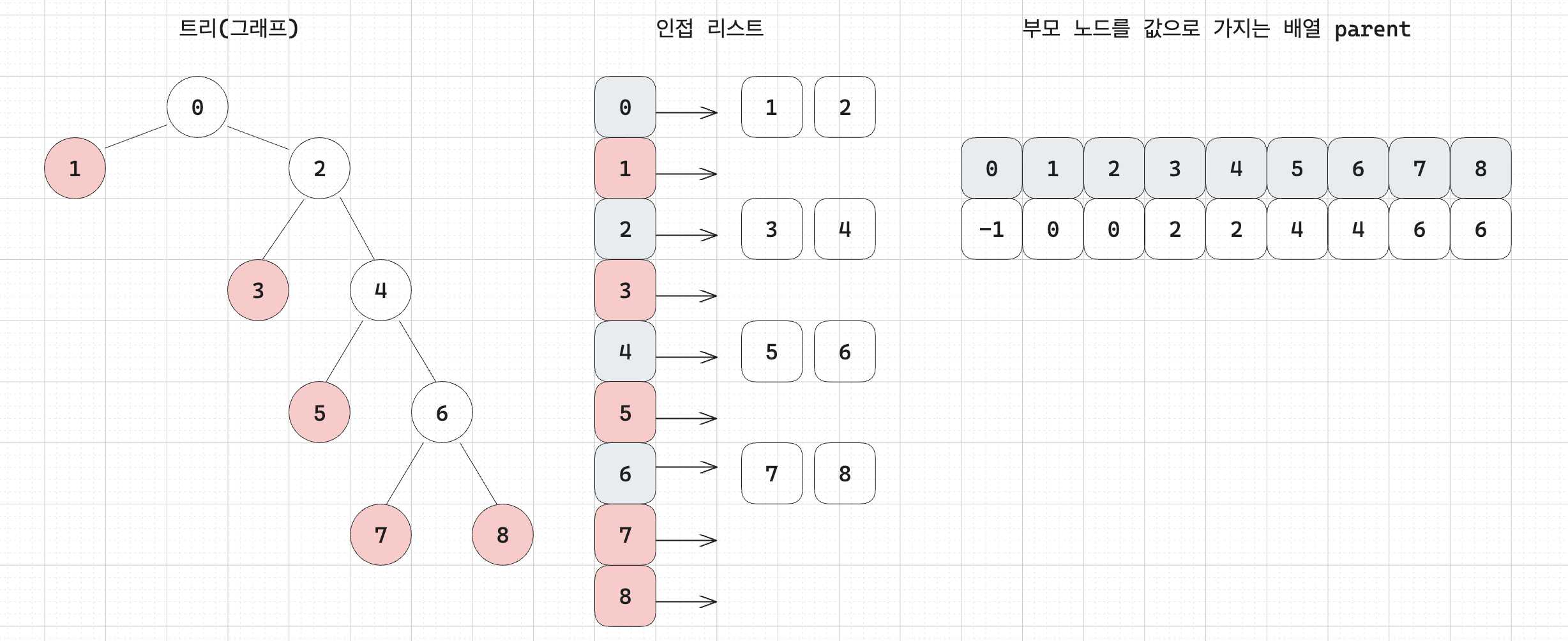
b. 삭제할 노드부터 시작해서 DFS 을 수행하면서 리프 노드의 개수(minusCnt)를 세고 만나는 노드의 자식 노드들을 모두 삭제한다.
여기서는 리프노드의 개수가 3개이다.
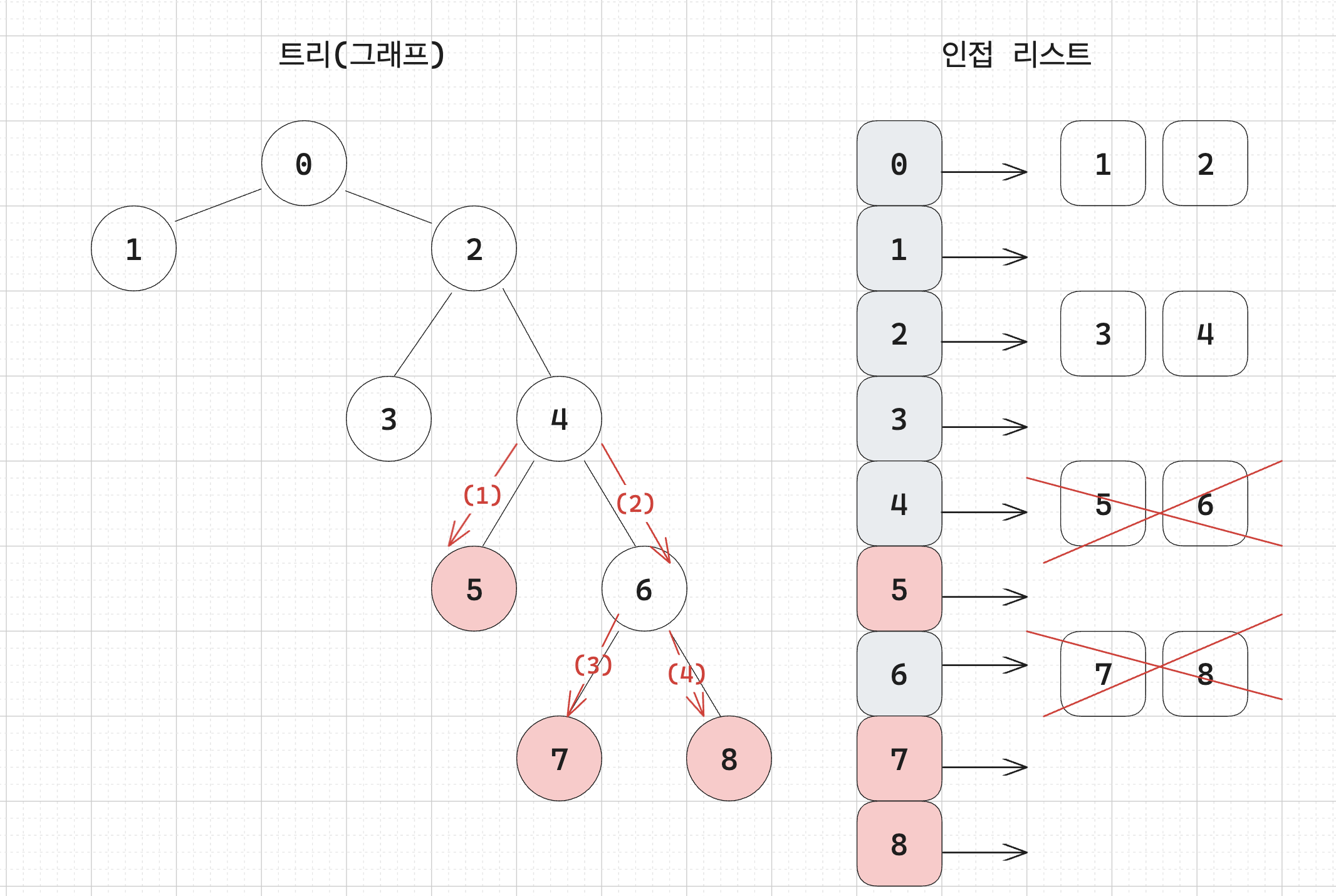
c. 삭제할 노드(4) 의 부모 노드가 자식을 오직 하나만 가지고 있는지 확인한다.
만약 오직 하나만 가지고 있다면 삭제할 노드의 부모 노드도 리프노드가 되기 때문에 leafCnt 에 1을 더해주어야 한다.
이 예시에서는 삭제할 노드의 부모노드가 자식 노드를 여러 개 가지고 있기 때문에 1을 더해주지 않아도 된다.
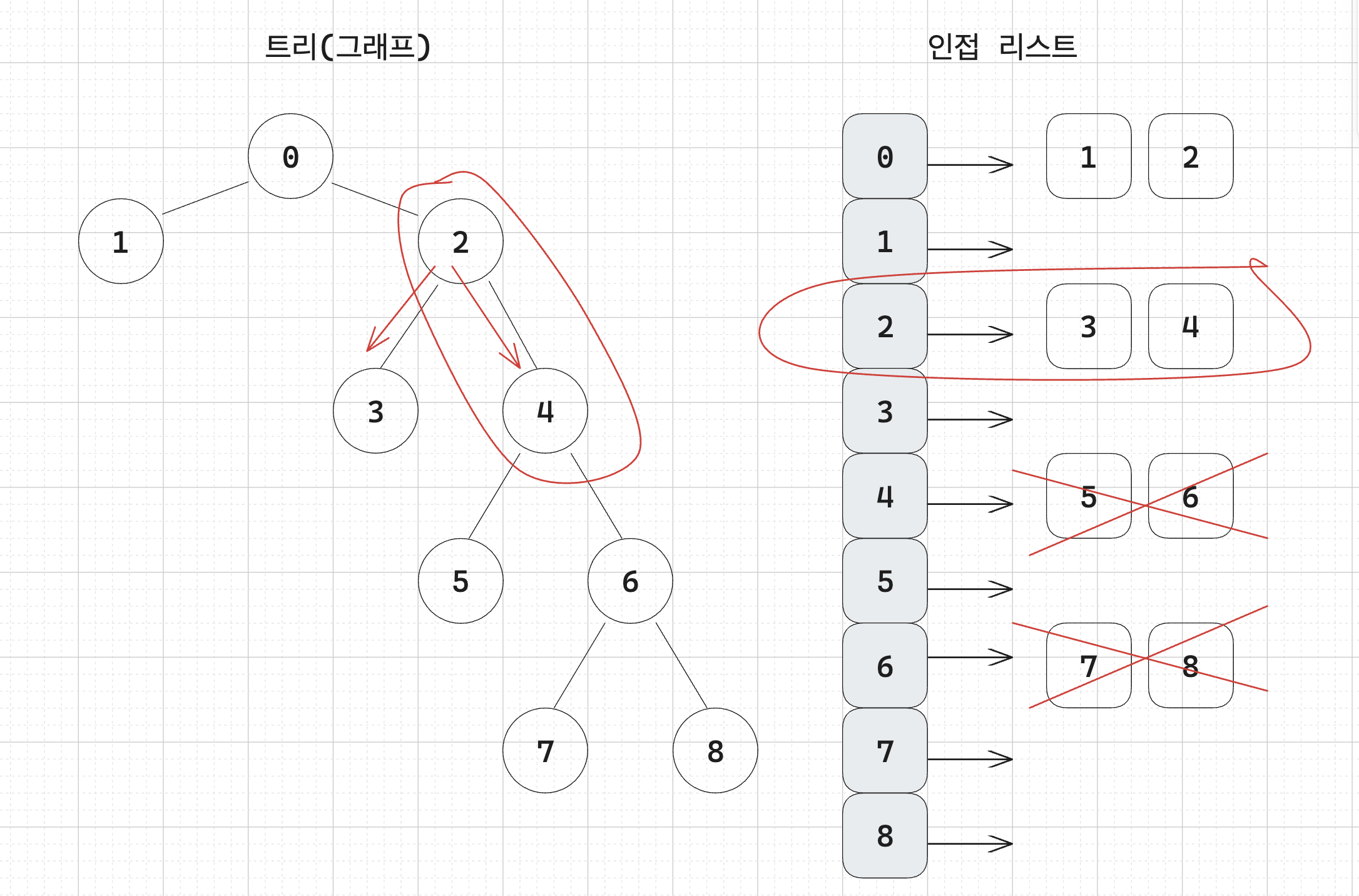
d. 위에서 구한 결과에 따라 leafCnt - minusCnt 의 값을 출력한다.
3. 슈도코드
N: 노드 개수
graph: 인접 리스트 Queue<Ingeer>[]
인접 리스트 데이터 입력받기. 방향성을 갖는 그래프로.
노드를 삭제하기 전에 트리에서 리프 노드의 개수를 모두 구해서 저장.
삭제할 노드부터 DFS 탐색.
삭제한 노드의 부모 노드가 오직 하나의 자식만을 가지고 있었다면 그 부모 노드도 리프노드가 됨.
처음 세었던 리프노드의 개수와 후에 minusCnt 을 사용해서 최종 리프 노드의 개수 계산.
최종 리프노드의 개수 출력
// dfs 함수
dfs(int node){
node 가 자식을 갖지 않으면(인접 노드가 없으면) minusCnt++;
for( 모든 자식(인접노드) nextNode 에 대해서){
dfs(자식)
}
그래프에서 현재 node 를 clear 하기
}4. 코드
public class BaekJun1068 {
static Queue<Integer>[] graph;
static int N, removeNode, leafCnt, minusCnt;
static int[] parent;
public static void main(String[] args) throws IOException {
input();
getFirstLeafCnt();
dfsFunc(removeNode);
getLastLeafCnt();
System.out.println(leafCnt);
}
private static void input() {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
graph = new LinkedList[N];
parent = new int[N];
for (int i = 0; i < N; i++) {
graph[i] = new LinkedList<>();
}
for (int i = 0; i < N; i++) {
int temp = sc.nextInt();
if (temp == -1) {
continue;
}
parent[i] = temp;
graph[temp].add(i);
}
removeNode = sc.nextInt();
}
private static void getFirstLeafCnt() {
for (int i = 0; i < N; i++) {
if (graph[i].isEmpty()) {
leafCnt++;
}
}
}
static void dfsFunc(int node) {
if (graph[node].isEmpty()) {
minusCnt++;
}
for (int nextNode : graph[node]) {
dfsFunc(nextNode);
}
graph[node].clear();
}
private static void getLastLeafCnt() {
if (graph[parent[removeNode]].size() == 1) {
leafCnt++;
}
leafCnt = leafCnt - minusCnt;
}
}
다른 풀이
1. 문제 분석
'리프 노드를 어떻게 제거하는가' 가 핵심입니다. 리프 노드를 탐색하는 탐색 알고리즘을 수행할 때 제거하는 노드가 나왔을 때 탐색을 종료하는 아이디어를 적용하면 실제 리프노드를 제거하는 효과를 낼 수 있습니다. 이 아이디어를 접목해서 문제에 접근해 봅시다.
2. 손으로 풀기
a. 인접 리스트로 트리 데이터를 구현합니다. 이번에는 단뱡향 그래프가 아니라 양방향으로 구현합니다.
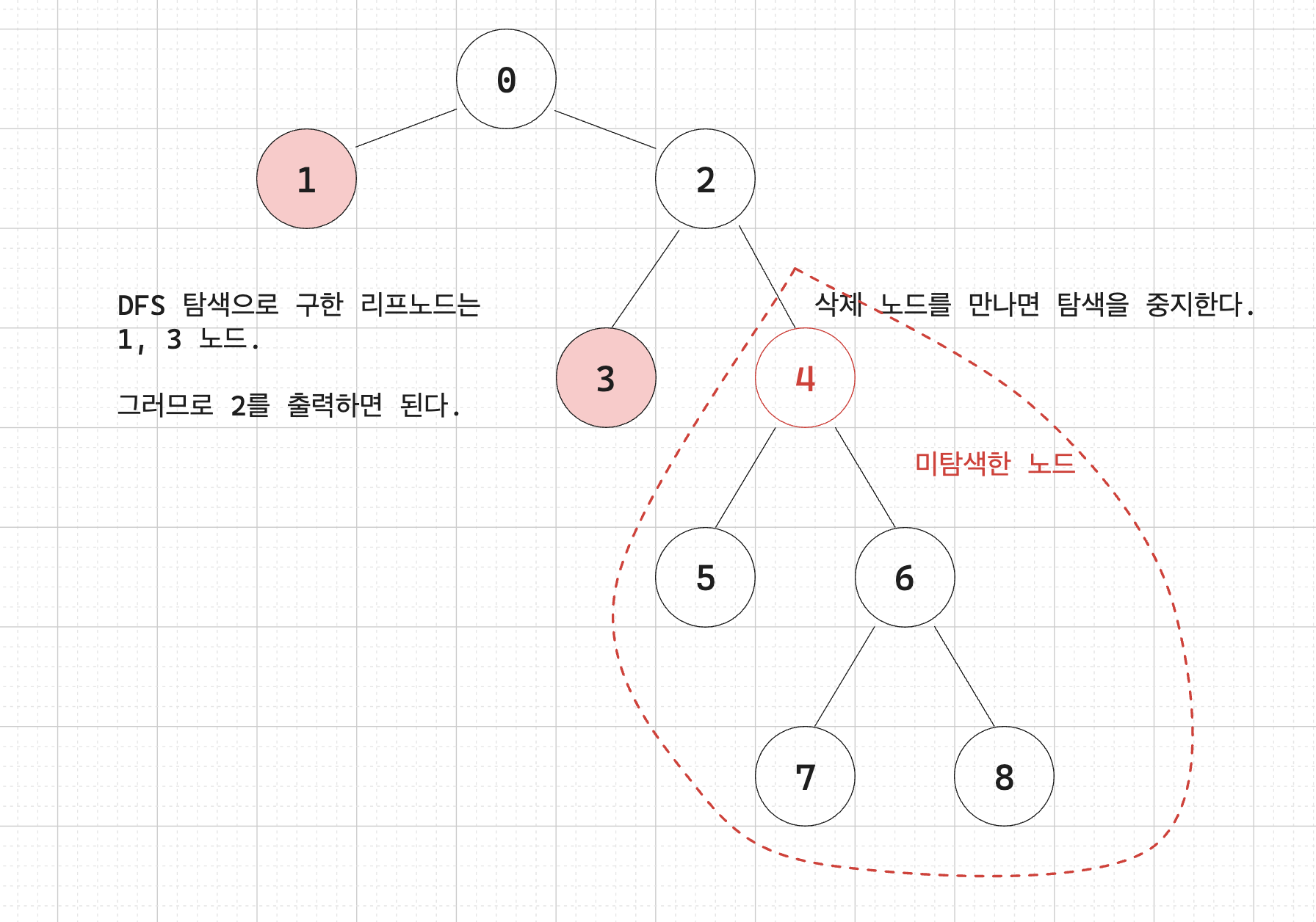
b. DFS 혹은 BFS 탐색을 수행하면서 리프 노드의 개수를 셉니다. 제거 대상을 만났을 때는 그 아래 자식 노드들과 관련된 탐색은 중지합니다.
3. 슈도코드
N: 노드 개수
tree: 트리 데이터 저장 인접 리스트
visited: 방문 기록 저장 배열
answer: 리프 노드 개수 저장 배열
deleteNode: 삭제 노드
tree 인접리스트에 데이터 초기화.
if(deleteNode 가 0 이면) 모두 삭제됨. 0을 출력하고 종료.
else dfs(루트 노드)
answer 출력
dfs(int node){
현재 노드 방문 체크
for(node 의 인전 노드 nextNode 탐색){
nextNode 가 방문하지 않았고 삭제 노드가 아닐 때
자식 노드 개수 증가
dfs(nextNode)
}
망냑 자식 노드의 개수가 0 이면 answer 변수 증가.
}4. 코드
public class BaekJun1068Book {
static ArrayList<Integer>[] tree;
static boolean[] visited;
static int ans, deleteNode, root;
public static void main(String[] args) {
input();
if (deleteNode == root) {
System.out.println(0);
} else {
dfsFunc(root);
System.out.println(ans);
}
}
private static void input() {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
tree = new ArrayList[N];
visited = new boolean[N];
root = 0;
for (int i = 0; i < N; i++) {
tree[i] = new ArrayList<>();
}
for (int i = 0; i < N; i++) {
int p = sc.nextInt();
if (p != -1) {
tree[i].add(p);
tree[p].add(i);
} else {
root = i;
}
}
deleteNode = sc.nextInt();
}
static void dfsFunc(int node) {
visited[node] = true;
int childCnt = 0;
for (int nextNode : tree[node]) {
if (!visited[nextNode] && nextNode != deleteNode) {
childCnt++;
dfsFunc(nextNode);
}
}
if (childCnt == 0) {
ans++;
}
}
}
다른 풀이 방법에서 트리 구조에서 루트 노드부터 DFS 나 BFS 탐색을 시작해서 삭제해야 하는 노드를 만났을 때 탐색을 종료하는 아이디어를 기억하는 것이 중요할 것 같네요.
'Java > 코딩테스트' 카테고리의 다른 글
| [JAVA] 이진 트리 백준 BOJ 1991 전위 순회, 중위 순회, 후위 순회 (0) | 2023.08.28 |
|---|---|
| [JAVA] 최소 신장 트리 알고리즘 자바 백준 BOJ 1197, 17472, 1414 (2) | 2023.08.24 |
| 플로이드-워셜 알고리즘 자바 백준 BOJ 11404, 11403 (1) | 2023.08.21 |
| 벨만 포드 알고리즘 자바 백준 BOJ 11657, 1219 (0) | 2023.08.18 |
| 우선순위 큐를 이용한 다익스트라 알고리즘 자바 백준 BOJ 1735, 1916, 1854 (0) | 2023.08.17 |