'Do it! 알고리즘 코딩테스트 자바 편' 교재로 공부한 내용을 정리했습니다
구간 합
구간 합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 것이다. 코딩 테스트에서 자주 사용되므로 잘 알아둡시다.
먼저 합 배열이 무엇인지 정의합시다. 만약 배열 A 가 있을 때 합 배열 S는 아래와 같다.
S[i] = A[0] + A[1] + A{2] + … A[i-1] + A[i]
즉, S[i] 는 A[0] 부터 A[i] 까지의 합이다.
합 배열은 기존 배열을 전처리한 배열이라고 할 수 있다. 만약 이렇게 합 배열을 구해 놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N) 에서 O(1) 으로 줄어든다.
예를 들어서 A[i] ~ A[j] 까지의 배열 합을 구해야 한다고 합시다.
합 배열 없이 구한다면 배열이 i번째 인덱스부터 시작해서 하나하나 다 더해야 하므로 O(N) 가 된다.
하지만 합 배열을 미리 구해놓았다면 단순히 S[j] - S[i-1] 연산을 수행하면 되며 이는 시간복잡도가 O(1+1) = O(2) = O(1) 이 된다.
- 합 배열 S 만드는 공식 : S[i] = S[i-1] + A[i]
- i 에서 j 까지 구간 합 공식 : S[j] - S[i-1]
합 배열과 구간 합 공식을 적재적소에 활용하면 코딩 테스트에서 시간 복잡도를 줄이는 데 큰 도움이 될 것이다.
바로 백준 문제 11659 번, 11660 번, 10986 번을 풀어봅시다.
백준 11659번
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
- 문제 분석
- 수의 개수와 합을 구해야 하는 횟수는 최대 100,000 이다.
- 게다가 구간마다 합을 매번 계산하면 계산의 횟수가 100,000 * 100,000 = 10,000,000,000 ,100억(?)까지 나온다.
- 그런데 문제의 시간 제한은 1초이므로 구간마다 합을 매번 계산하면 안 되고 구간 합을 이용해야 한다.
- 손으로 풀기
- N개의 수를 입력받고 동시에 합 배열 S 을 생성한다. S[i] = S[i-1] + A[i]
- 구간 i ~ j 가 주어지면 구간 합을 구하는 공식으로 출력한다. S[j] - S[i-1]
- 슈도 코드
suNo(숫자 개수), queryNo(질의 개수) 저장.
for(suNo 만큼 반복하기){
합 배열 생성하기 (S[i] = S[i-1] + A[i]
}
for(queryNo 만큼 반복하기){
query 범위 받기 (i ~ j)
구간 합 출력하기 ( S[j] - S[i-1] )
4. 구현
public class BaekJoon11659 {
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
// 첫번째 줄 입력받고 저장
int suNo = Integer.parseInt(stringTokenizer.nextToken()); // 수의 개수
int queryNo = Integer.parseInt(stringTokenizer.nextToken()); // query 개수
long[] S = new long[suNo + 1]; // 합 배열 생성
// 배열 값 입력 받기, 합 배열 S 초기화하기.
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 1; i <= suNo; i++) {
S[i] = S[i - 1] + Integer.parseInt(stringTokenizer.nextToken());
}
// 합을 구할 구간 입력 받고 구하기
for (int q = 0; q < queryNo; q++) {
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
int i = Integer.parseInt(stringTokenizer.nextToken());
int j = Integer.parseInt(stringTokenizer.nextToken());
System.out.println(S[j] - S[i - 1]);
}
}
}
버퍼링 기능을 제공하는 BufferedReader 라는 보조 스트림 클래스를 사용했으며, 문제의 입력과 출력의 형식 때문에 StringTokenizer 라는 보조 스트림 클래스를 사용했다.
- BufferedReader (Buffered 스트림)
- 내부적으로 8,192 바이트 크기의 배열을 가지고 있으며 더 빠르게 입출력을 실행하도록 버퍼링 기능을 제공한다. 한 바이트나 한 문자 단위로 처리할 때보다 훨씬 빠르게 처리할 수 있다.
- 여기서는 InputStreamReader 을 감싸서 보조 스트림으로 사용되고 있다.
- StringTokenizer
- 어떤 문자열을 구분자로 쪼개주는 클래스. 이렇게 쪼개진 문자열은 토큰(token) 이라고 부른다.
- 생성자는 아래와 같다.생성자 설명
이 클래스는 잘 알아두자!셍성자 설명 public StringTokenizer(String str) 전달된 매개변수 str을 default인 delim 로 분리한다. 여기서 기본 delimiter 는 공백 문자들이다! public StringTokenizer(String str,
String delim);구분자(delimiter) delim 을 직접 지정하여 str을 분리한다. public StringTokenizer(String str,
String delim, boolean returnDelims);str을 특정 delim 으로 분리시킬 때 그 delim 까지 token으로 포함할지를 결정합니다. returnDelims 가 true 이면 포함하고, false 이면 포함하지 않습니다.
백준 11660번
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
- 문제분석
- 이 문제 역시 query의 개수가 최대 100,000 이므로 구간 합 배열을 사용하자. 달라진 점은 딱 하나이다. original 배열과 구간 합 배열이 1차원에서 2차원으로 확장된 것이다.
- 2차원 합 배열 D[X][Y] 이면
D[X][Y] = 원본 배열의 (0,0) 에서부터 (X,Y) 까지의 사각형 영역 안에 있는 수의 합.
- 손으로 풀기
- 먼저 원본 배열 A 와 구간 합 배열 D 을 그리면
여기서 아래 식이 나온다.
D[i][1] = D[i-1][1] + A[i][1]
D[1][j] = D[1][j-1] + A[1][j]
- 먼저 원본 배열 A 와 구간 합 배열 D 을 그리면

2. 이를 통해서 나머지 2차우너 구간 합 배열을 채운다.
D[i][j] 의 값을 채우는 구간 합 공식 D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]

3. 구간 합 배열을 이용하기 전에 query 에 대한 답을 도출하기 위한 과정을 예를 들어서 살펴보자. 만약 query 가 2 2 3 4 이면. (2,2) ~ (3,4) 구간을 구해야 한다.

즉, D(3,4) 에서 D(1,4) 와 D(3,1) 를 빼야 한다. 그리고 다시 D(1,1) 을 더한다.
⇒ D[3][4] - D[1][4] - D[3][1] + D[1][1] = 27
이것을 일반화해보자. 아래와 같은 결과가 나온다.
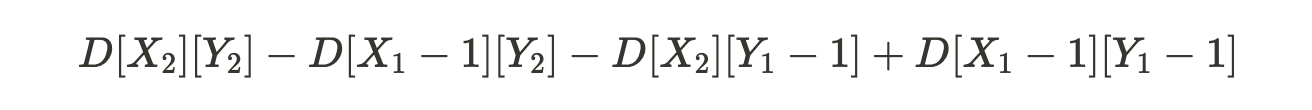
3. 슈도코드
N(배열 크기) M(query 수) 입력받고 저장
for(N 만큼 반복) {
for(N 만큼 반복) {
원본 배열 저장하기
}
}
for(N만큼 반복) {
for(N만큼 반복){
합 배열 저장하기
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
}
}
for(M만큼 반복){
query 계산, 출력
result = 위에서 구한 식
}
4. 구현
public class BaekJoon11660 {
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
// N, M (배열 크기, query 수 ) 입력 받고 저징
int N = Integer.parseInt(stringTokenizer.nextToken());
int M = Integer.parseInt(stringTokenizer.nextToken());
int A[][] = new int[N + 1][N + 1]; // original array
for (int i = 1; i < N + 1; i++) {
// 배열 값 입력받기(한 행마다)
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
// 각 토큰을 위치에 맞게 저장.
for (int j = 1; j < N + 1; j++) {
A[i][j] = Integer.parseInt(stringTokenizer.nextToken());
}
}
int D[][] = new int[N + 1][N + 1]; // 구간 합 배열
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < N + 1; j++) {
// 구간 합 구하기
D[i][j] = D[i][j - 1] + D[i - 1][j] - D[i - 1][j - 1] + A[i][j];
}
}
for (int i = 0; i < M; i++) {
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
// (x1, y1) ~(x2, y2)
int x1 = Integer.parseInt(stringTokenizer.nextToken());
int y1 = Integer.parseInt(stringTokenizer.nextToken());
int x2 = Integer.parseInt(stringTokenizer.nextToken());
int y2 = Integer.parseInt(stringTokenizer.nextToken());
// 구간 합 배열로 query 의 결과 답 출력
int result = D[x2][y2] - D[x1 - 1][y2] - D[x2][y1 - 1] + D[x1 - 1][y1 - 1];
System.out.println(result);
}
}
}
백준 10986 번
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
- 문제 분석
- 10⁶ 수의 모든 구간 합을 구해야 하므로 1초 안에 연산하기 어렵다. 여기서도 구간 합 배열을 사용해야 한다. 이 나머지 합 문제 풀이의 핵심 아이디어는 아래와 같다.
- (A + B) % C = ( (A%C) + (B %C) ).
즉, 특정 구간 수들의 나머지 연산을 더해 나머지 연산을 한 값과 이 구간 합의 나머지 연산을 한 값은 동일하다. - 구간 합 배열을 이용한 식 S[i] - S[j] 는 원본 배열의 i + 1 부터 j 까지의 구간 합이다.
- S[i] % M = S[j] % M 이라면 ( S[j] - S[i] ) % M = 0. ↔ S[i] % M - S[j] % M = 0
즉, 구간 합 배열의 원소를 M 으로 나눈 나머지로 하는 배열 S’ 을 만들고 위 식의 경우처럼 ‘S[i] 와 S[j]’ 같은 (i, j) 쌍을 찾으면 원본 배열에서 i+1 부터 j 까지의 구간 합이 M 으로 나누어 떨어진다는 것을 알 수 있다.
- (A + B) % C = ( (A%C) + (B %C) ).
- 10⁶ 수의 모든 구간 합을 구해야 하므로 1초 안에 연산하기 어렵다. 여기서도 구간 합 배열을 사용해야 한다. 이 나머지 합 문제 풀이의 핵심 아이디어는 아래와 같다.
- 손으로 풀기

3. 슈도 코드
N(수열의 개수) 입력받고 저장
M (나누어 떨어져야 하는 수) 입력받고 저장
S (합 배열) 선언.
C 선언. (같은 나머지의 인덱스를 카운트하는 배열)
result 선언 (답)
for(i -> 1 ~ N){
S[i] = S[i-1] + A[i] // 합 배열 저장
}
for(i -> 0 ~ N){
remainder = S[i] % M // 합 배열을 M 으로 나눈 나머지 값
if(remainder == 0) -> result++;
C[remainder] 의 값 1 증가
}
for(i -> 0 ~ M){
C[i](i 가 나머지인 인덱스의 개수) 에서 2가지를 뽑는 경우의 수를 정답에 더하기
// C[i] 개 중 2개를 뽑는 경우의 수 계산 공식 C[i] * (C[i]-1) / 2
}
print(result)
4. 구현
public class BaekJoon10986 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); // 수열의 개수
int M = sc.nextInt(); // 나누어 떨어져야 하는 수
long[] S = new long[N]; // 합 배열
long[] C = new long[M]; // 같은 나머지 인덱스 카운트
long result = 0;
S[0] = sc.nextInt();
// 수열 합 배열 S
for (int i = 1; i < N; i++) {
S[i] = S[i - 1] + sc.nextInt();
}
for (int i = 0; i < N; i++) {
int remainder = (int) (S[i] % M);
if (remainder == 0) { // 0 ~ i 까지의 구간 합 자체가 0인 경우. 카운트
result++;
}
C[remainder]++; // 나머지와 같은 인덱스인 위치에 하나씩 증가시키기.
// 결과적으로 각 나머지가 나온 횟수가 배열에 저장될 것임.
}
for (int i = 0; i < M; i++) {
if (C[i] > 1) {
// 나머지가 것들의 수를 알고 있다. 이 중 2개를 뽑는 경우의 수를 더하기
result = result + C[i] * (C[i] - 1) / 2;
}
}
System.out.println(result);
}
}'Java > 코딩테스트' 카테고리의 다른 글
| [Java] 코딩테스트 BufferedReader, BufferedWriter 을 쓰는 이유 (0) | 2023.05.21 |
|---|---|
| 스택 & 큐 - 자바 백준 스택수열: 1874 오큰수: 17298 (0) | 2023.05.21 |
| 자바 코딩 테스트 - 슬라이딩 윈도우. 백준 12891, 11003 문제 (1) | 2023.01.05 |
| 자바 코딩 테스트 - 투 포인터. 백준 2018, 1940, 1253 (0) | 2023.01.03 |
| 자바 코딩 테스트 - 배열과 리스트, 백준 11720, 1546 문제 (0) | 2023.01.02 |