DFS(깊이 우선 탐색) 자바 백준 11724, 2023, 13023

Java/코딩테스트

DFS(깊이 우선 탐색) 자바 백준 11724, 2023, 13023

sh1mj1 2023. 7. 17. 17:19

DFS(Depth-First Search)

깊이 우선 탐색은 DFS(Depth-First Search). 그래프 완전 탐색 기법 중 하나입니다.

그래프의 시작 노드에서 출발하여 탐색할 한쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘입니다.

기능	특징	시간 복잡도 (V: 노드 수, E: 에지수)
그래프 완전 탐색	재귀함수로 구현 스택 자료 구조 이용	O(V+E)

DFS 는 실제 구현 시 재귀함수를 이용하므로 Stack Overflow 에 유의해야 합니다.

깊이 우선 탐색을 응용하여 풀 수 있는 문제는 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬이 있습니다.

DFS 는 한번 방문한 노드를 다시 방문하면 안되므로 노드 방문 여부를 체크할 배열이 필요합니다.

그래프는 인접 리스트 혹은 인접 행렬로 표현합니다. 그리고 DFS 는 LIFO(Last-in First-Out: 후입 선출) 특성을 가지기 때문에 스택을 이용하여 설명합니다.

(실제로는 DFS 는 코딩테스트에서는 재귀함수로 구현되는 경우가 더 빈번하지만 설명의 편의를 위해 스택을 이용합니다.)

1. DFS 을 시작할 노드를 정한 후 사용할 자료구조 초기화

먼저 인접 리스트로 그래프를 표현하고, 방문 배열 초기화합니다. 그리고 시작 노드를 스택에 push 합니다. 스택에 시작 노드를 1 로 삽입할 때 해당 위치의 방문 배열을 체크합니다.

2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 push

pop 을 수행하여 노드를 꺼냅니다. 꺼낸 노드를 탐색 순서에 기입하고 인접 리스트의 인접 노드를 스택에 삽입하여 방문배열을 체크합니다. 방문 배열은 T, T, T, F, F, F 가 됩니다.

3. 스택 자료 구조에 값이 없을 때까지 반복앞선 과정을 스택 자료구조에 값이 없을 때까지 반복합니다.

탐색 순서: 1 → 3 → 4 → 6 → 2 → 5

이 때 이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심입니다.스택에 노드를 삽입할 때 방문 배열을 체크하고 스택에서 노드를 뺄 때 탐색 순서에 기록하며 인접 노드를 방문 배열과 대조하여 살펴봅니다.

백준 11724

11724번: 연결 요소의 개수

첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어

www.acmicpc.net

1. 문제 분석

연결 요소는 에지로 연결된 노드의 집합이며, 한번의 DFS 가 끝날 때까지 탐색한 모든 노드의 집합을 하나의 연결 요소로 판단할 수 있습니다. DFS 탐색을 해나가면서 방문 노드를 초기화하고 방문한 노드는 탐색을 하지 않도록 하면 됩니다.

노드의 최대 개수가 1,000, 에지 개수는 최대 499,500 이므로 시간 복잡도는 꽤 여유 있습니다.

2. 손으로 풀기

a. 그래프를 인접리스트로 저장하고 방문 배열도 초기화합니다. 방향이 없는 그래프이기 때문에 양쪽 방향으로 에지를 모두 저장합니다.

b. 임의의 시작점에서 DFS 을 수행합니다. 그림에서처럼 1을 시작점으로 정했습니다. 탐색을 마친 후에는 방문한 노드는 1, 2, 5 가 됩니다. 탐색 순서는 1 → 2 → 5 가 됩니다.

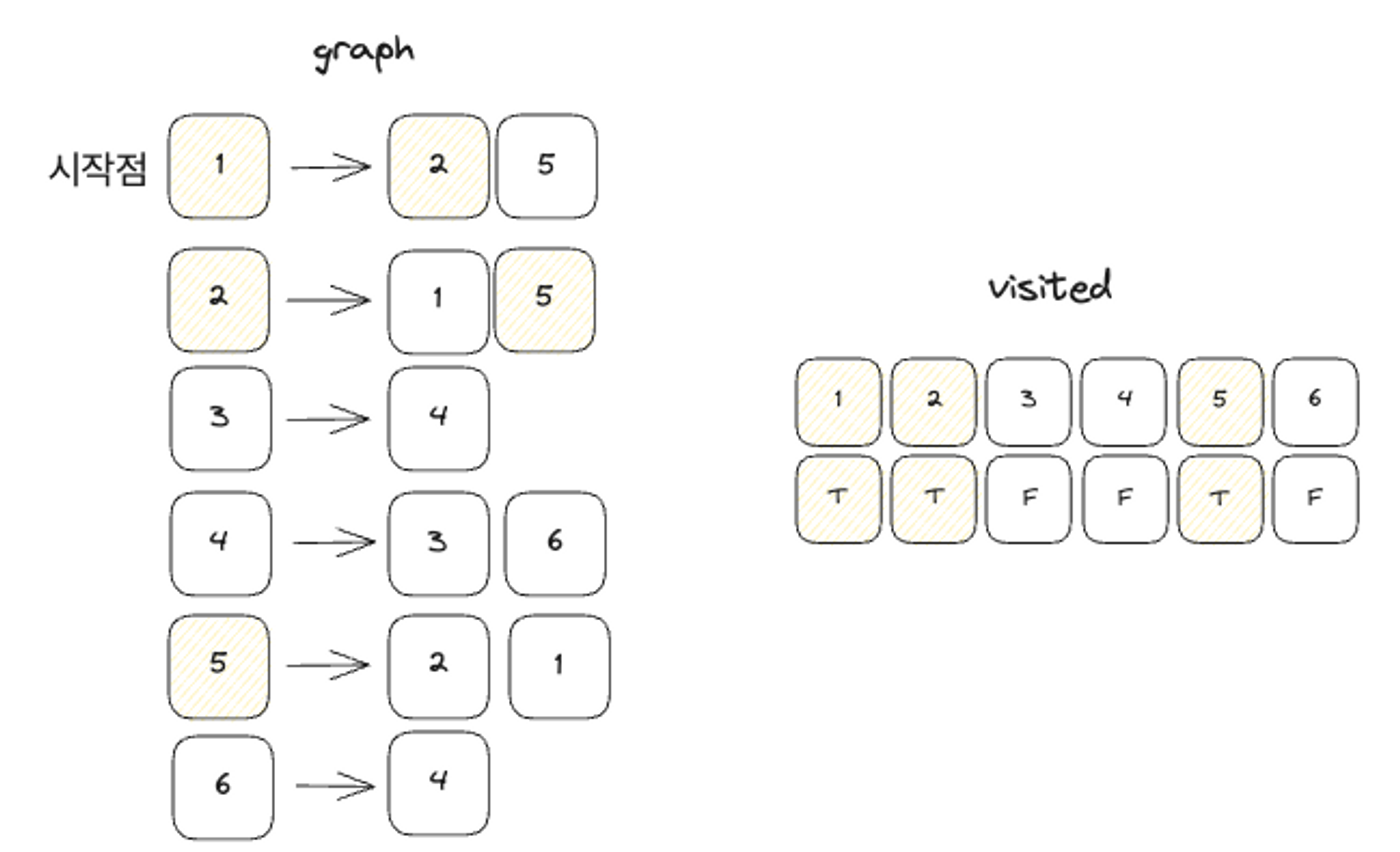
c. 한번의 DFS 가 끝납니다. 그런데도 아직 방문하지 않은 노드들이 많이 남아있습니다. 다른 시작점을 정해서 DFS 탐색을 합니다. 이 때 이미 방문한 노드라면 그 노드를 시작점으로 DFS 을 수행하지 않아도 됩니다. 즉, 방문하지 않은 노드만 시작점으로 하여 DFS 을 수행합니다. 시작점이 3번 노드가 되겠지요.

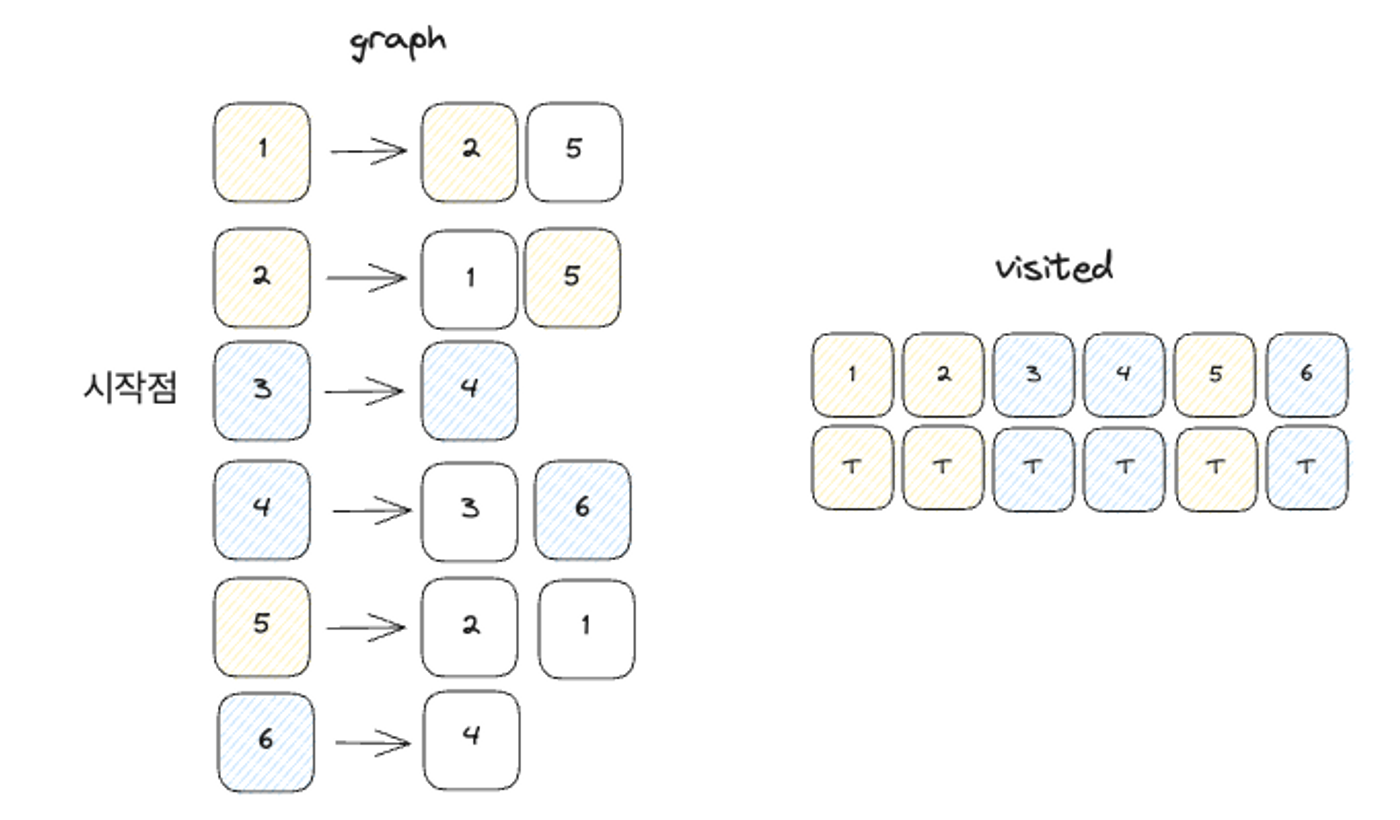
d. a ~ c 의 과정을 통하여 총 2번의 DFS 가 진행되었다는 것을 알 수 있습니다. 즉, 연결 요소 개수는 2개입니다. 만약 그래프가 모두 연결되어 있었다면 DFS 는 1번 실행되었을 것입니다. 모든 노드를 탐색하기 위해 실행한 DFS의 실행 횟수가 연결 요소의 개수와 같습니다.

3. 슈도코드

N: 노드 개수, M: 에지개수
graph: 인접 리스트로 그래프 표현
visited: 방문 배열
for(N){ graph 에 각 ArrayList 초기화 } 
for(M){ 그래프 데이터 저장. 무방향 그래프인 것을 주의 }

for(N){
	if(!visited[node]){
		연결요소++;
		dfs
	}
}

// dfs method
dfs(int node){
	이미 방문했으면 return;
	visited 배열에 현재 노드 방문 기록
	현재 노드의 연결 노드 중 방문하지 않은 노드로 dfs 실행(재귀함수)
}

4. 코드

public class Main{

    static ArrayList<Integer>[] adjacencyList;
    static boolean[] visited;
    public static void main(String[] args) throws IOException {
        BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());

        // N: 노드의 개수, M: 에지의 개수, count: 연결 요소의 개수
        int N = Integer.parseInt(stringTokenizer.nextToken());
        int M = Integer.parseInt(stringTokenizer.nextToken());
        int count = 0;

        // 그래프를 인접 리스트로 표현, 방문 배열, 인접 리스트 초기화
        adjacencyList = new ArrayList[N + 1];
        visited = new boolean[N + 1];

        for (int i = 1; i < N + 1; i++) {
            adjacencyList[i] = new ArrayList<>();
        }
        for (int i = 0; i < M; i++) {
            stringTokenizer = new StringTokenizer(bufferedReader.readLine());
            int u = Integer.parseInt(stringTokenizer.nextToken());
            int v = Integer.parseInt(stringTokenizer.nextToken());
            adjacencyList[u].add(v);
            adjacencyList[v].add(u);
        }

        for (int i = 1; i < N + 1; i++) {
            if (!visited[i]) {
                count++;
                dfsMethod(i);
            }
        }

        System.out.println(count);


    }

    private static void dfsMethod(int node) {
        if (visited[node]) {
            return;
        }
        visited[node] = true;

        for (int adjacencyNode : adjacencyList[node]) {
            dfsMethod(adjacencyNode);
        }

    }
}

백준 2023

https://www.acmicpc.net/problem/2023

2023번: 신기한 소수

수빈이가 세상에서 가장 좋아하는 것은 소수이고, 취미는 소수를 가지고 노는 것이다. 요즘 수빈이가 가장 관심있어 하는 소수는 7331이다. 7331은 소수인데, 신기하게도 733도 소수이고, 73도 소수

www.acmicpc.net

1. 문제 분석

DFS 는 재귀함수의 형태를 띄고 있습니다. 재귀함수에 자릿수 개념을 붙여 구현합니다. 또 문제 조건에 맞춰서 탐색할 수 있는 노드를 미리 제한하는 게 좋습니다.

2. 손으로 풀기

소수는 약수가 1과 자기 자신인 수를 말합니다. 1은 제외하고 2, 3, 5, 7 등이 됩니다.

자릿수가 한 개인 소수는 2, 3, 5, 7이므로 가장 높은 자리 수는 2, 3, 5, 7 만 가능합니다. 이 수부터 탐색을 시작하면 됩니다. 이어서 자릿수가 두개인 수 X = (현재 수 * 10 + 다음 수) 에 대해서 소수인지 판단하고 만약 소수라면 재귀함수로 자릿수를 하나 늘립니다. 다음 수는 항상 홀수여야 합니다. 만약 짝수라면 X 가 항상 2를 약수로 가지게 되므로 1, 3, 5, 7, 9 만 가능합니다. 즉, 두 번째 깊이에서부터는 1, 3, 5, 7, 9 중에서만 탐색하면 됩니다.

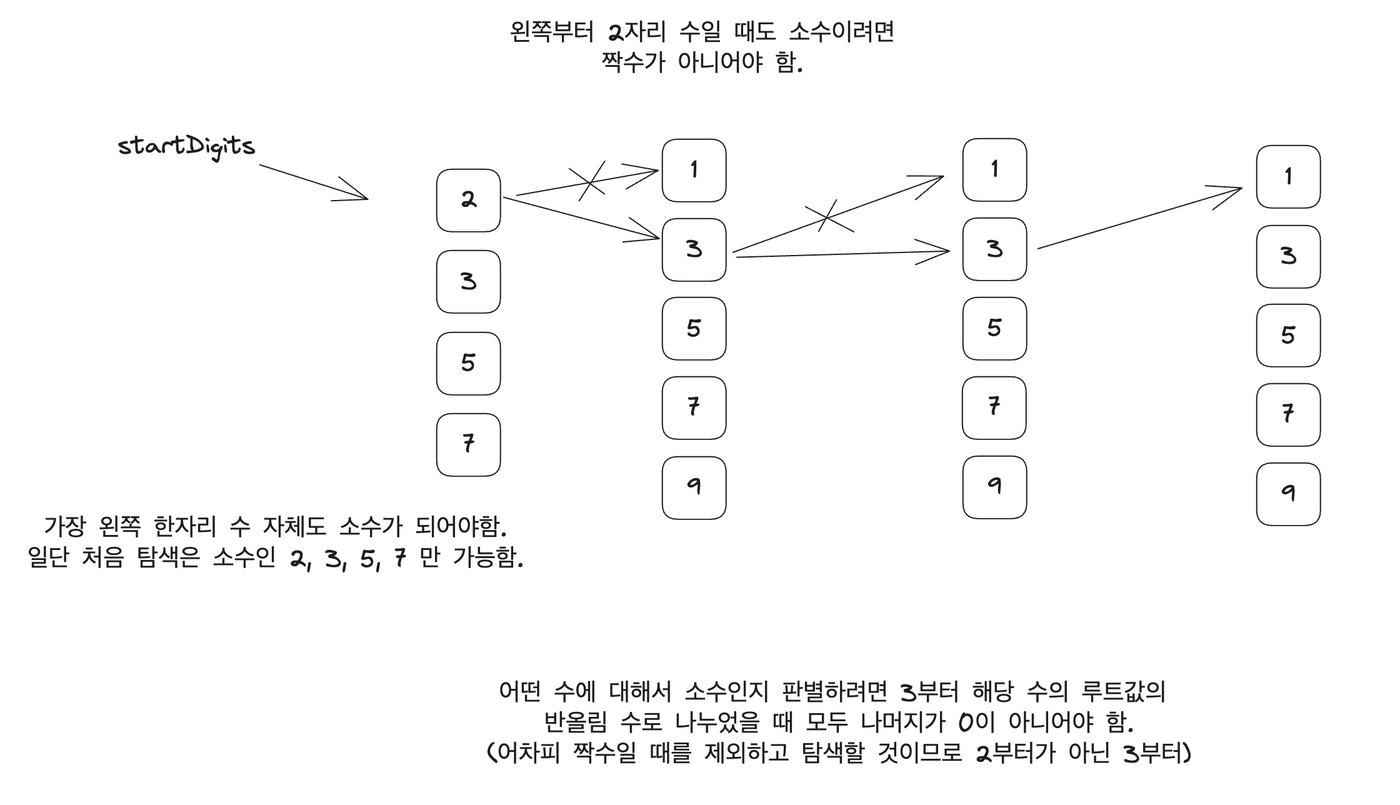
그렇게 깊이가 N 일 때 해당 수가 소수라면 출력하고 탐색을 종료합니다.

구현이 재귀함수로 이루어지므로 탐색을 종료하면 그 다음 함수가 호출되어 탐색을 지속하게 되겠죠.

그림에서처럼 N = 4 일 때 탐색은 2 → 21(소수X 탐색 종료) → 23(소수 O 더 깊게 탐색) → 231(소수 X 탐색 종료) → 233(소수 O 더 깊게 탐색) → 2331(소수 O, 깊이 = 4. 탐색 종료) → 2333 …

여기서 특정 수를 소수인지 탐색하기 위해서는 3부터 해당 수의 제곱근까지의 수를 반복하여 나누었을 때 나머지가 항상 0이 아니면 소수라고 판별됩니다.

(보통 소수를 판별하기 위해서는 ‘에라토스테네스의 체’ 를 이용하지만 여기서는 위처럼 해도 충분히 시간 안에 가능합니다.)

3. 슈도코드

N : 자리수, 
DFS 실행. (숫자 2, 3, 5, 7 에 대해서)

// DFS method
DFS(숫자, 자리수(깊이) ){
	깊이++
	if(자리수 > N) {수 출력, return)
	
	for(새로운 수 1, 3, 5, 7, 9 반복){
		int 현재 수 = 숫자 * 10 + 새로운 수
		int rootVal = 현재 수의 제곱근
		
		현재 수가 소수인지 판별. 소수이면 반복문 종료
		
		만약 현재 수가 소수이면
		DFS(현재 수, 깊이)
}

4. 코드

public class Main {
    static int[] startDigits = {2, 3, 5, 7};
    static int[] digits = {1, 3, 5, 7, 9};
    static int N;
    static boolean isPrimary;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();

        for (int i : startDigits) {
            int depth = 1;
            dfs(i, depth);
        }

    }

    static void dfs(int num, int depth) {
        depth++;
        if (depth > N) {
            System.out.println(num);
            return;
        }
        for (int i : digits) {
            isPrimary = true;
            int currentNum = num * 10 + i;
            int rootVal = (int) Math.sqrt(currentNum);

            for (int j = 3; j <= rootVal; j++) {
                if (currentNum % j == 0) {
                    isPrimary = false;
                    break;
                }
            }

            if (isPrimary) {
                dfs(currentNum, depth);
            }
        }
    }
}

백준 13023

https://www.acmicpc.net/problem/13023

13023번: ABCDE

문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.

www.acmicpc.net

1. 문제 분석

사람의 수, 즉 노드의 수가 최대 2,000 이고, 에지의 수는 최대 2,000, 시간 제한이 2초이므로 시간에서 어느정도 자유롭습니다.

한 노드에서 DFS 로 완전 탐색을 진행하면 O(2,000 + 2,000) 이고, 모든 노드에 대해서 실행을 한다면 O(2,000 * (2,000 + 2,000)) = O(2,000 * 4,000) = O(8,000,000) 이므로 여유롭습니다.

2. 손으로 풀기

그래프를 위처럼 인접 리스트로 표현한 후 모든 노드에 대해서 DFS 탐색을 하면 됩니다.

이 때 주의할 점은 두가지입니다.

친구 관계라는 점은 무방향 그래프라는 것
끝까지 탐색을 하고 나서 깊이가 5가 되지 않은 경우, 방문했던 노드를 다시 미방문 처리해야 합니다.

이 중 두번째 주의할 점에 대해서 구체적으로 설명하자면 아래와 같습니다. 아래와 같은 그래프가 있다고 합시다.

탐색 순서가 0 → 1 → 3 → 2 라고 합시다. 이 경우에 깊이가 4일 때 탐색이 끝나게 됩니다.

그리고 다시 3번 노드에서의 dfs 호출부로 돌아가서 4번 노드로 갑니다. (0 → 1 → 3 → 4) 이 경우에도 탐색이 깊이 4로 끝납니다.

다시 1번 노드에서의 dfs 호출부로 돌아갑니다. 그런데 이 때 인접 노드가 모두 방문되어 있으므로 탐색이 불가하여 깊이가 5가 되지 않는다고 판단하며 프로그램이 끝나게 됩니다.

하지만 실제로는 탐색을 0 → 1 → 4 → 3 → 2 순서로 하게 된다면 깊이가 5인 것을 찾아낼 수 있습니다.

이러한 것을 방지하기 위해서 우리는 깊이가 5가 아닌 상태로 탐색이 끝났을 때의 해당 노드에서는 방문을 하지 않았다고 처리를 해주어야 합니다. 즉, DFS 메소드의 마지막 부분에 방문하지 않았다고 표시를 해주는 겁니다.

구체적인 시나리오는 아래와 같습니다.

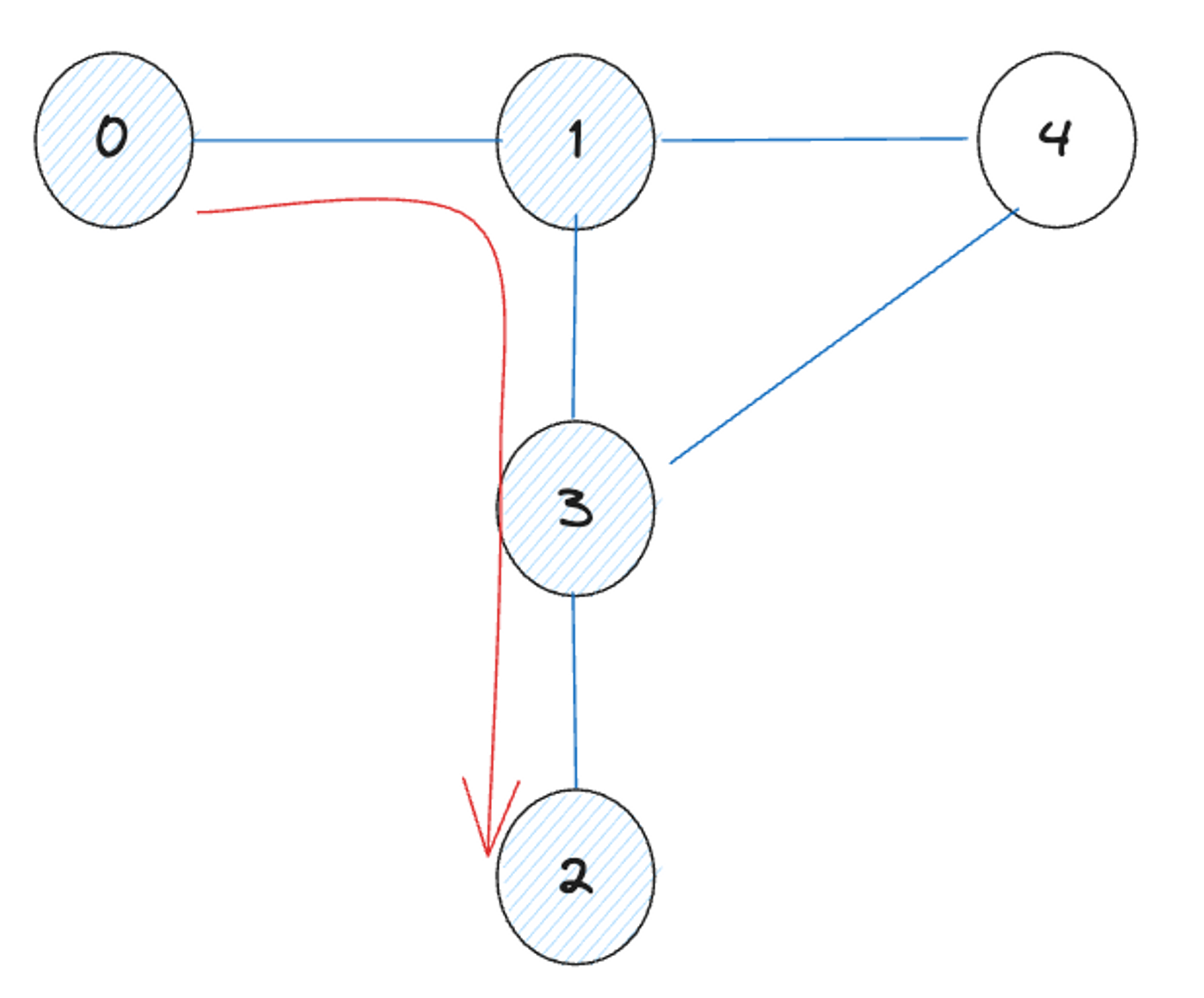
0 → 1 → 3 → 2. (색칠 노드: 방문함, 색이 없는 노드: 미방문)

탐색 실패했으므로 되돌아감. 2를 미방문 처리

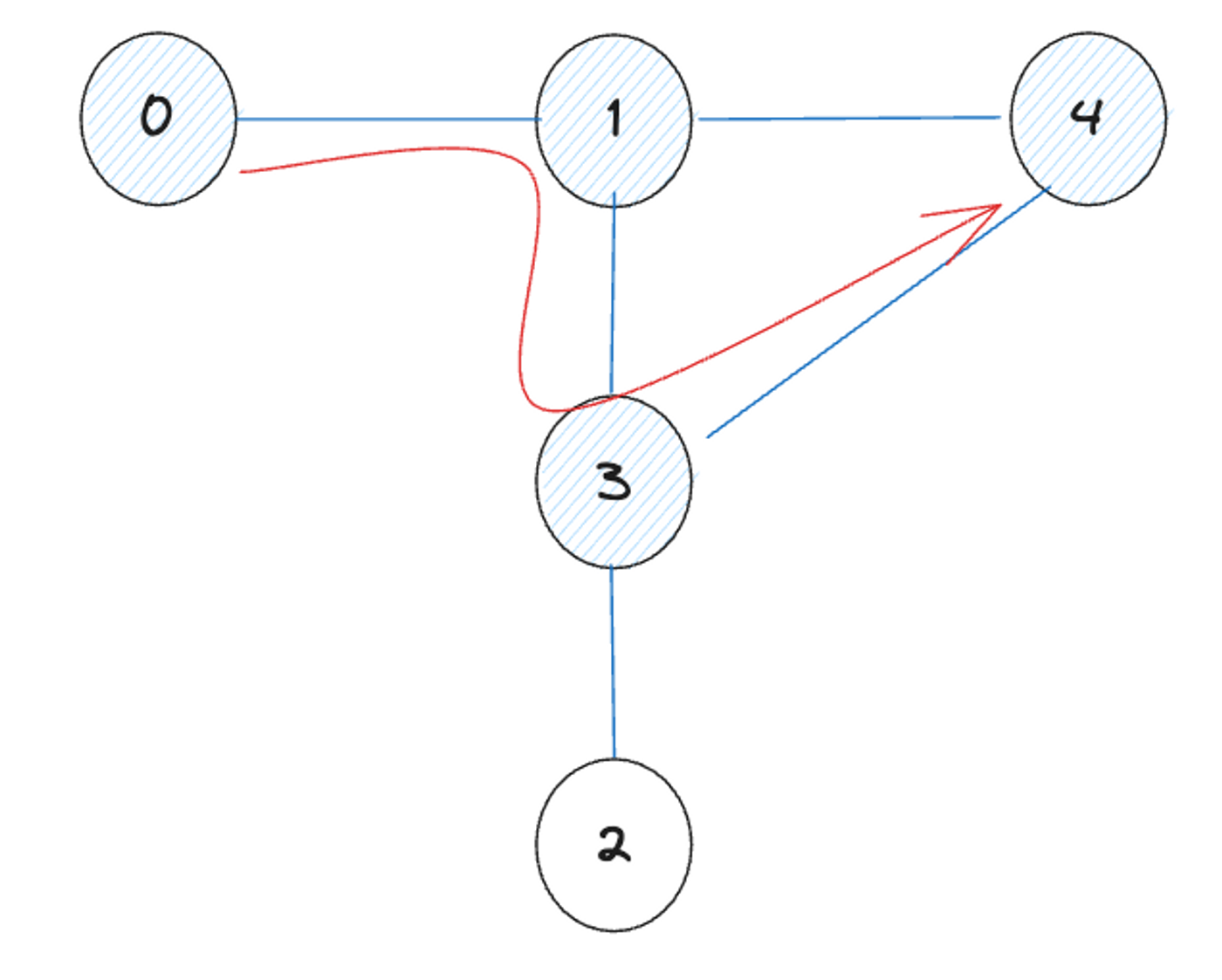
0 → 1 → 3 → 4

탐색 실패했으므로 되돌아감. 4를 미방문 처리

0 → 1

3번 노드에서 2, 4 에 모두 방문했었으므로 탐색 실패, 되돌아감. 3을 미방문 처리

0 → 1 → 4 → 3 → 2

1번 노드에서 이번에는 4번 노드로 탐색. 그리고 순서대로 탐색했을 때 깊이가 5인 것 탐색 성공.

3. 슈도코드

N, M: 노드개수, 에지 개수
graph, visited: 인접리스트, 방문배열
depth, isSatisfied: 깊이, 조건 만족 여부 

graph:Integer형 ArrayList 을 원소로 하는 ArrayList
visited 초기화

for(모든 노드에 대해서){
	depth = 1;
	dfs(노드, depth)
	if(isSatisfied 가 1이면){
		break;
	}
}
sout(isSatisfied)

dfs(노드, 깊이){
	현 노드가 이미 방문했으면 리턴.
	현 노드 방문 체크

	if(깊이 == 5){isSatisfied =1; 리턴}
	
	현재 노드의 인접 노드에 대해서 방문하지 않았으면 
	dfs(인접 노드, 깊이 + 1)
	
	// 현 노드에서 탐색을 모두 했을 시
	현 노드 미방문으로 체크
}

4. 코드

public class BaekJun13023Self {
    static ArrayList<Integer>[] graph;
    static boolean[] visited;
    static int depth;
    static int isSatisfied = 0;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());
        graph = new ArrayList[N];
        visited = new boolean[N];

        for (int i = 0; i < N; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            graph[u].add(v);
            graph[v].add(u);
        }

        for (int i = 0; i < N; i++) {
            depth = 1;
            dfs(i, depth);
            if (isSatisfied == 1) {
                break;
            }
        }
        System.out.println(isSatisfied);
    }

    static void dfs(int node, int depth) {
        if (visited[node]) {
            return;
        }

        visited[node] = true;

        if (depth == 5) {
            isSatisfied = 1;
            return;
        }

        for (int adjNode : graph[node]) {
            if (!visited[adjNode]) {
                dfs(adjNode, depth + 1);
            }
        }
        visited[node] = false;

    }
}

'Java > 코딩테스트' 카테고리의 다른 글

이진 탐색 (Binary Search) 자바 백준 1920 2343 1300 (3)	2023.07.19
BFS(너비 우선 탐색) 자바 백준 1260, 2178, 1167 (0)	2023.07.18
버블 정렬 - 자바 백준 수 정렬하기: 2750, 버블 소트: 1377 (0)	2023.06.01
자바 PriorityQueue (0)	2023.05.29
스택 & 큐 - 자바 백준 카드2: 2164 절댓값 힙: 11286 (0)	2023.05.29

현재글DFS(깊이 우선 탐색) 자바 백준 11724, 2023, 13023

공부하고 작업한 내용을 정리하고 기록하는 블로그

스프링, 타임리프, 안드로이드, 코틀린, Java, 예외, 데이터베이스, Android, 알고리즘, 코테, 자바 스프링, 서블릿, boj, 백준, db, MVC, 오브젝트, kotlin, 자바, 트랜잭션,

Today :
Yesterday :

sh1mj1_log