BFS(Breadth-First Search)
BFS(너비 우선 탐색)은 DFS 와 마찬가지로 그래프를 완전 탐색하는 방법 중 하나로 시작 노드에서 출발해서 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘입니다.
| 기능 | 특징 | 시간복잡도 (V: 노드 수, E: 에지 수) |
|
그래프 완전 탐색
|
FIFO 탐색 Queue 자료구조 이용 | O(V+E) |
FIFO(선입선출 방식)으로 탐색하므로 큐를 이용하여 구현합니다.
너비 우선 탐색은 탐색 시작 노드와 가까운 노드를 우선시하여 탐색하므로 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장합니다.
BFS 구현은 아래 3단계로 설명할 수 있습니다.
1. BFS 시작 노드를 정한 후 자료구조 초기화
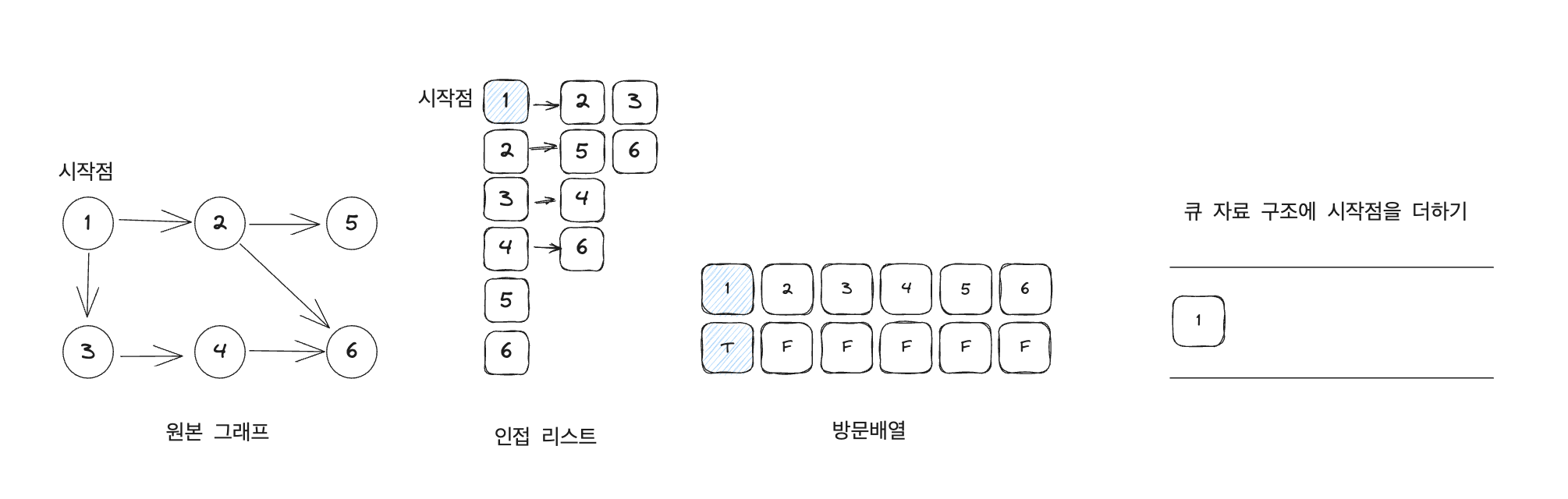
BFS 도 DFS 처럼 방문했던 노드는 다시 방문하지 않습니다. 그래서 방문 노드 체크 배열이 필요합니다. 그래프를 인접리스트 또는 인접행렬로 표현하는 것도 동일합니다. 여기서는 인접 리스트를 사용하여 설명합니다.
차이점은 큐를 사용하여 구현하는 것입니다.
2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입
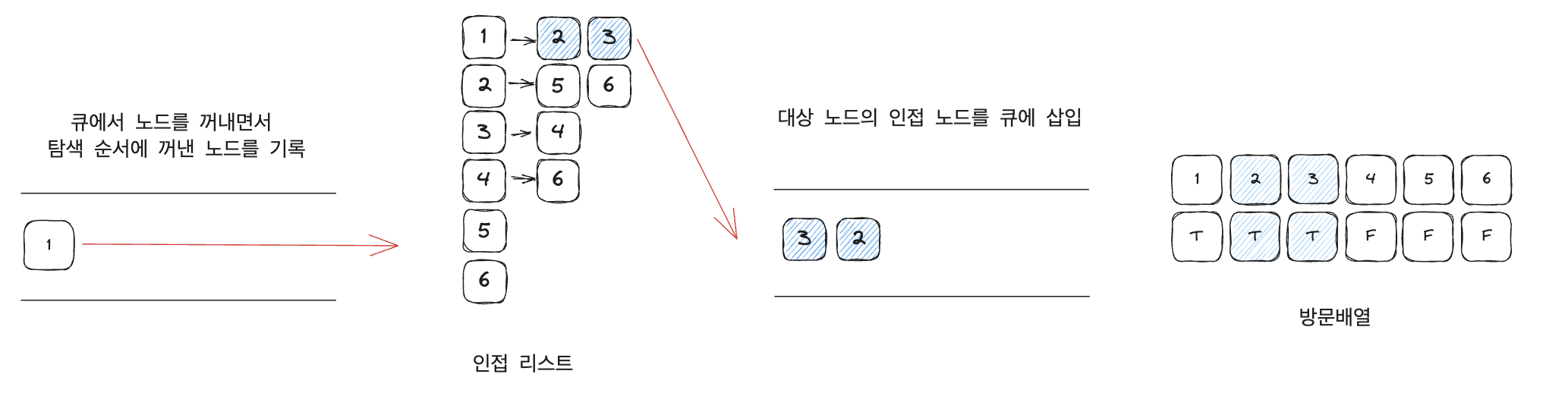
큐에서 노드를 꺼내면서 인접 노드를 큐에 삽입합니다. 이 때 방문 배열을 체크하여 True 인 노드는 큐에 삽입하지 않습니다. 또한 큐에서 꺼낸 노드는 탐색 순서에 기록합니다.
현재 상태에서는 방문배열의 노드 2, 3 이 true 이지만 아직 방문하지는 않았습니다. 실제로 방문한 노드는 큐에서 pop 한 1뿐입니다.
3. 큐 에 값이 없을 때까지 반복
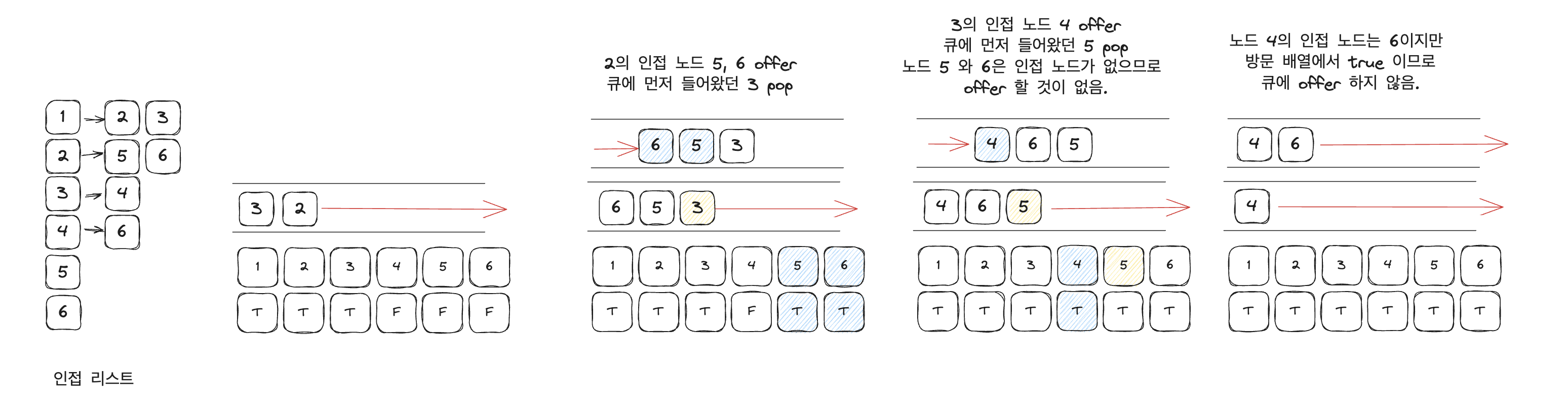
큐에 노드가 없을 때까지 앞선 과정을 반복합니다. FIFO 방식으로 탐색하므로 탐색 순서가 이전 포스팅의 DFS 와는 다릅니다.
위 그림처럽 2, 3 순서로 노드를 꺼내면서 인접 노드를 큐에 넣습니다. 노드 2의 인접 노드 5, 6 은 아직 방문 배열에서 false 이므로 모두 큐에 넣습니다. 노드 3의 인접노드 4도 역시 같은 이유로 삽입합니다.
노드 5, 6 을 꺼낼 때는 인접 노드가 없으므로 따로 노드를 삽입하지 않습니다. 노드 4의 인접노드 6은 방문배열에서 true 이므로 삽입하지 않습니다.
이렇게 큐가 완전히 비어질 때까지 같은 행위를 반복합니다.
결과적으로 최종 탐색 순서는 1 -> 2 -> 3 -> 5 -> 6 가 됩니다.
백준 문제 3문제 정도 풀어봅시다.
백준 1260 DFS 와 BFS
https://www.acmicpc.net/problem/1260
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
1. 문제 분석
아주 간단한 DFS, BFS 문제입니다. 단지 방문할 수 있는 노드가 여러 개일 경우 노드 번호가 작은 것을 먼저 방문해야 한다는 조건이 달려있을 뿐입니다.
2. 손으로 풀기
a. 인접 리스트 저장

b. DFS 을 실행하면서 방문 배열 체크와 탐색 노드 기록 수행. 문제 조건에서 작은 번호의 노드부터 탐색한다고 했으므로 인접 노드를 오름차순으로 정렬해야 합니다.
이 때 Collections.sort() 메소드를 사용하거나 인접 노드들을 우선순위 큐를 사용하여 집어 넣으면 될 것 같습니다.
그리고 나서 DFS 재귀 함수를 호출하면 됩니다.
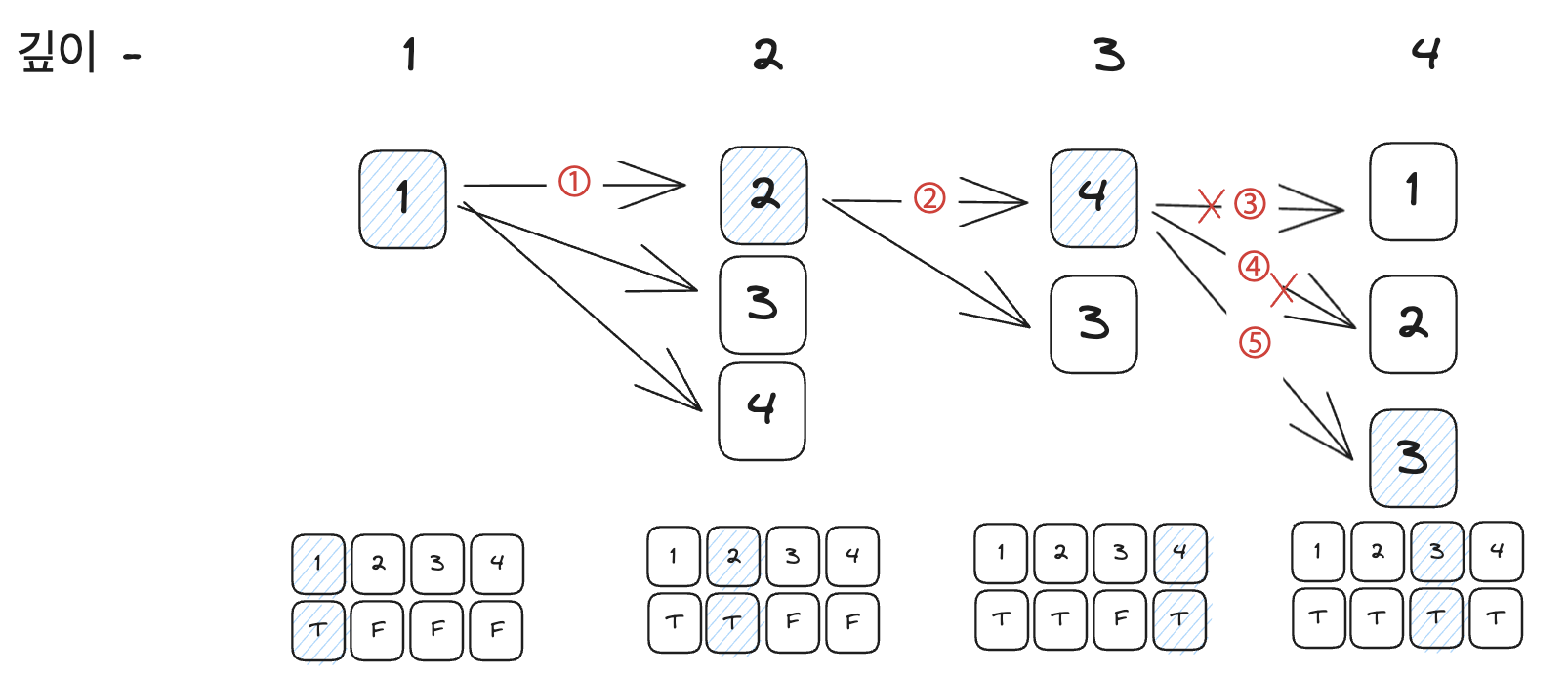
위 그림의 화살표의 숫자처럼 탐색이 될 것입니다.
탐색 순서는 1 -> 2 -> 4 -> 3 이 됩니다.
c. BFS 을 실행합니다.
큐를 이용합니다.
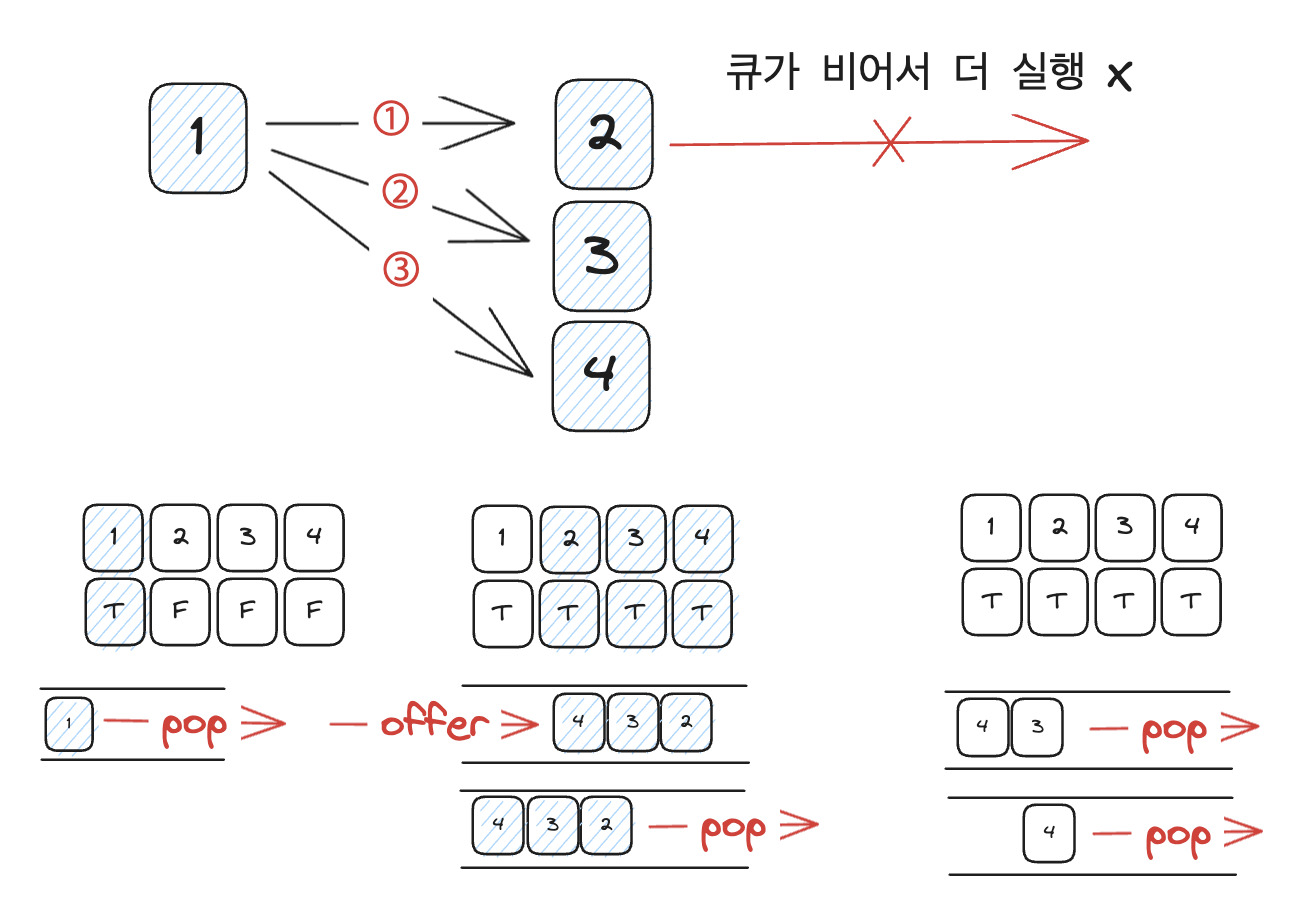
이번에도 위 그림의 화살표처럼 탐색이 될 것입니다.
탐샌 순서는 1 -> 2 -> 3 -> 4 가 됩니다.
3. 슈도코드
N, M, startNode: 노드 개수, 에지 개수, 시작노드
graph: 그래프를 저장할 인접 리스트. ArrayList<Integer> 을 원소로 갖는 ArrayList
visited: 방문 체크 배열
graph 에 노드, 에지 초기화
노드와 관련된 에지 정렬
visited 초기화
DFS 실행
visited 초기화
BFS 실행
// DFS method
DFS{
현재 노드 출력
visited 에 기록
현재 노드의 인접 노드 중 미방문 노드를 DFS
}
// BFS method
BFS{
큐 선언, 시작 노드 삽입, visited 에 기록
while(큐가 완전히 빌 때까지){
큐에서 poll
poll 한 노드 출력
현재 노드의 인접 노드 중 미방문 노드를 큐에 offer, visited 에 기록
}
}4. 코드
import java.io.*;
import java.util.*;
public class Main {
static ArrayList<Integer>[] graph;
static boolean[] visited;
static BufferedWriter bw;
static Queue<Integer> queue;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int startNode = Integer.parseInt(st.nextToken());
graph = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
graph[u].add(v);
graph[v].add(u);
}
br.close();
for (int i = 1; i <= N; i++) {
Collections.sort(graph[i]);
}
visited = new boolean[N + 1];
dfs(startNode);
bw.write("\n");
bw.flush();
visited = new boolean[N + 1];
queue = new LinkedList<>();
queue.offer(startNode);
visited[startNode] = true;
bfs();
bw.flush();
bw.close();
}
static void dfs(int node) throws IOException {
visited[node] = true;
bw.write(node + " ");
for (int adjNode : graph[node]) {
if (!visited[adjNode]) {
dfs(adjNode);
}
}
}
static void bfs() throws IOException {
while (!queue.isEmpty()) {
int node = queue.poll();
bw.write(node + " ");
for (int adjNode : graph[node]){
if (!visited[adjNode]) {
queue.offer(adjNode);
visited[adjNode] = true;
}
}
}
}
}
백준 2178 미로 탐색
https://www.acmicpc.net/problem/2178
2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net
1. 문제 분석
노드와 엣지인 N, M 의 최대가 100 이므로 크지 않아 시간 복잡도는 매우 여유롭습니다. 즉, 시간 제한은 크게 생각하지 않아도 됩니다.
출발지인 (1,1)에서 도착지 (N, M) 까지 이동할 때 지나야 하는 칸 수의 최소값을 찾아야 합니다. 이는 완전탐색을 진행하고 이 때 도착지가 몇번째 깊이에 있는지를 찾으면 됩니다. 따라서 BFS 을 사용하여 해결하면 됩니다.
이 문제에서 DFS 가 아닌 BFS 을 사용하는 것이 적합한 이유는 BFS 에서는 어떤 깊이의 노드들을 방문한 후에 다음 깊이로 넘어가기 때문입니다.
2. 손으로 풀기
문제의 예제 2번을 가지고 손으로 풀어보겠습니다.

처음 노드 1에서 BFS 탐색을 합니다.
위에서 파란색으로 칠해진 노드는 오른쪽 방향이나 아래 방향으로 이동할 수 있고 노란색 노드는 왼쪽, 오른쪽 , 위, 아래 방향으로 이동할 수 있습니다. 물론 이미 방문한 노드를 다시 방문하면 안되는 것도 고려해야 겠죠.
그렇다면 어떠한 노드에 대해서 위, 아래, 오른쪽, 왼쪽 방향으로 이동할 수 있다고, 즉, 인접노드가 4개라고 본 후 BFS 탐색을 진행합니다. 이 때 이미 방문한 노드는 탐색을 다시 진행하지 않도록 하고, N 𝘅 M (위에서는 4 𝘅 6) 의 그림에서 벗어나는 위치도 탐색에서 제외, 그리고 인접 노드의 값이 0 인 곳도 제외하는 조건문을 넣어서 진행하면 됩니다.
깊이에 따라 탐색을 그림으로 나타내면 아래와 같이 될 것입니다.

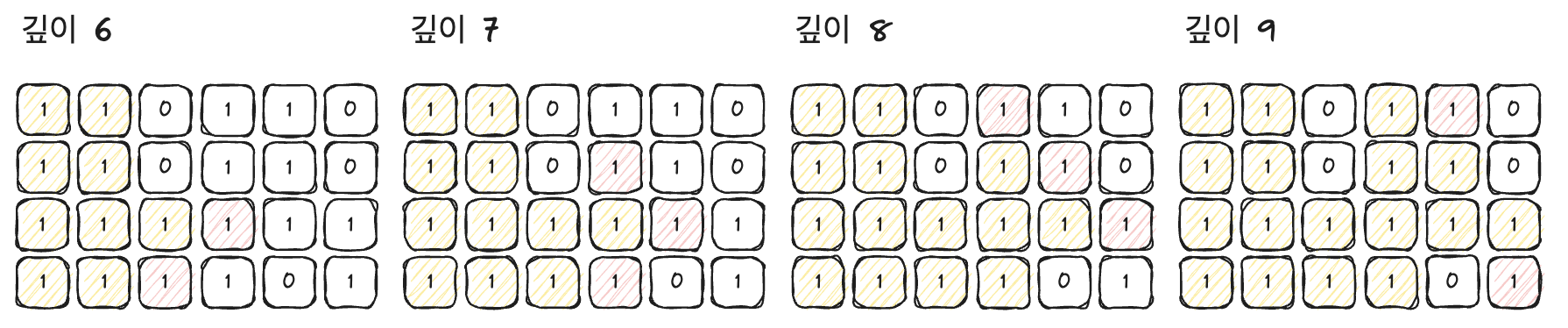
먼저 2차원 배열에 데이터를 저장한 후 (1, 1) 에서 BFS 을 실행합니다. 상, 하, 좌, 우 4 방향을 보면서 인접한 노드를 봅니다. 인접한 노드가 1이면서 아직 방문하지 않았다면, 그리고 그래프 안에 들어있다면 큐에 노드를 삽입합니다.
만약 그래프가 위처럼 4𝘅6 인데 (5, 7) 칸 같은 경우는 그래프 안에 있지 않은 것이지요.
그리고 방문했음을 표시할 때 2차원 방문 배열을 따로 선언하여 사용할 수도 있지만 그래프에서 노드의 값이 0 이면 방문할 수 없으므로 이미 방문한(큐에 삽입한) 노드의 값은 0 으로 바꾸어주면 더 간단히 구현할 수 있습니다.
도착지인 (N, M) 에서 BFS 을 종료합니다.
위 그림을 보면 깊이가 9일 때 도착 노드에 도착한 것을 알 수 있습니다. 이 때의 깊이가 9이기 때문에 출발지에서 도착지까지는 9의 값으로 도착할 수 있음을 알 수 있습니다.
3. 슈도코드
N, M: 인접 노드
graph: 2차원 배열, 여기에 노드의 값인 0, 1 저장.
queue: LinkedList 로 queue 을 구현한다.
depth = 1 // 깊이
queue 에 시작 노드 삽입.
시작 노드 방문 표시
bfs 실행
//bfs 메소드
while(큐가 비어있지 않으면){
큐에서 노드 curNode 를 poll 함.
만약 curNode 가 (N, M) 이라면 해당 반복문 종료. depth 출력
curNode 의 인접 노드 큐에 삽입.
// 이 때 미방문했으며 그래프 안에 있고 값이 1인 노드만 삽입.
// 인접 노드는 curNode 의 x 좌표에 dx[0 ~ 3], y 좌표에 dy[0 ~ 3] 을 더해서
curNode 을 방문함 표시. (해당 값일 0으로 변경)
depth++
}
4. 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class BaekJun2178Self {
static int N;
static int M;
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, 1, 0, -1};
static int[][] graph;
static Queue<Point> qu;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
graph = new int[N + 1][M + 1]; // (1, 1) -> (0, 0)
for (int i = 0; i < N; i++) {
char[] line = br.readLine().toCharArray();
for (int j = 0; j < M; j++) {
graph[i][j] = line[j] - '0';
}
}
qu = new LinkedList<>();
qu.offer(new Point(0, 0, 1));
graph[0][0] = 0; // 방문
bfs();
}
static void bfs() {
while (!qu.isEmpty()) {
Point curNode = qu.poll();
int curX = curNode.x;
int curY = curNode.y;
int curDepth = curNode.depth;
for (int i = 0; i < 4; i++) {
int adjNodeX = curX + dx[i];
int adjNodeY = curY + dy[i];
int adjNodeDepth = curDepth + 1;
if (adjNodeX >= 0 && adjNodeX < N && adjNodeY >= 0 && adjNodeY < M
&& graph[adjNodeX][adjNodeY] == 1) {
if (adjNodeX == N - 1 && adjNodeY == M - 1) {
System.out.println(adjNodeDepth);
return;
}
Point adjNode = new Point(adjNodeX, adjNodeY, adjNodeDepth);
qu.offer(adjNode);
graph[adjNodeX][adjNodeY] = 0;
}
}
}
}
static class Point {
int x;
int y;
int depth;
public Point(int x, int y, int depth) {
this.x = x;
this.y = y;
this.depth = depth;
}
}
}
슈도코드를 작성할 때는 위처럼 depth 변수를 static int 형으로 만들어서 사용하려고 했지만 아예 Point 라는 클래스 내부의 변수로 사용하는 것이 구현하는 중에 더 좋을 것 같다는 생각이 들어 해당 방법으로 구현했습니다.
백준 1167 트리의 지름
https://www.acmicpc.net/problem/1167
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
1. 문제 분석
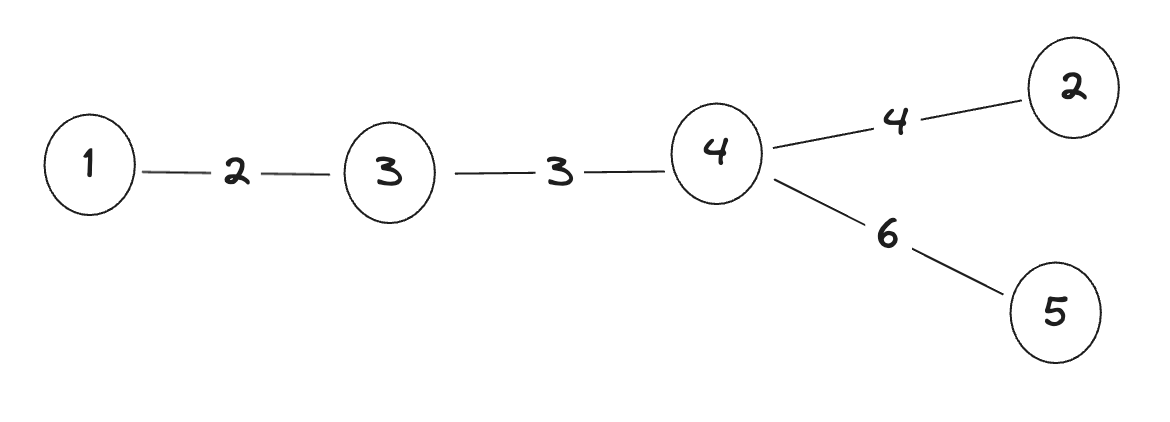
임의의 노드에서 완전탐색을 했을 때 가장 긴 경로를 찾는다고 해도 그 경로가 트리의 지름은 아닙니다. 위 그림을 예로 들면 3번 노드에서 완전 탐색을 통해서 가장 긴 경로의 거리를 찾는다고 하면 3 -> 4 -> 5 경로가 되고 이 때 총 거리는 3 + 6 = 9 가 됩니다.
물론 모든 노드에 대해서 한번씩 완전탐색하여 가장 긴 경로를 찾는 것도 방법이 될 수 있습니다.
그런데 노드의 개수가 100,000 이고, 에지는 문제의 입력에서는 주어지지 않았지만 이론상 𝘯C₂ = 100,000 * (100,000-1)/2 입니다. 즉, 최악의 경우 O(V+E) = O(100,000 + 4,999,950,000) = O(5,000,050,000) 가 되어 50억번의 연산으로 50초 정도의 시간이 소요됩니다. 이 시간은 문제의 시간 제한인 2초를 훨씬 넘는 시간이므로 다른 아이디어가 필요합니다.
핵심 아이디어는
"임의의 노드에서 가장 긴 경로로 연결되어 있는 노드는 트리의 지름에 해당하는 두 노드 중 하나이다"
입니다.
직접 손으로 노드 하나씩 잡아서 가장 긴 경로를 찾다보면 위 아이디어가 옳다는 것을 알 수 있습니다.
결론적으로 우리는 모든 노드에 대해 완전 탐색을 할 필요 없이 2 번의 완전탐색만으로도 결과를 구할 수 있습니다.
2. 손으로 풀기
1. 그래프를 인접 리스트로 저장합니다. (노드, 가중치) 를 표현하기 위한 클래스를 하나 만듭니다.
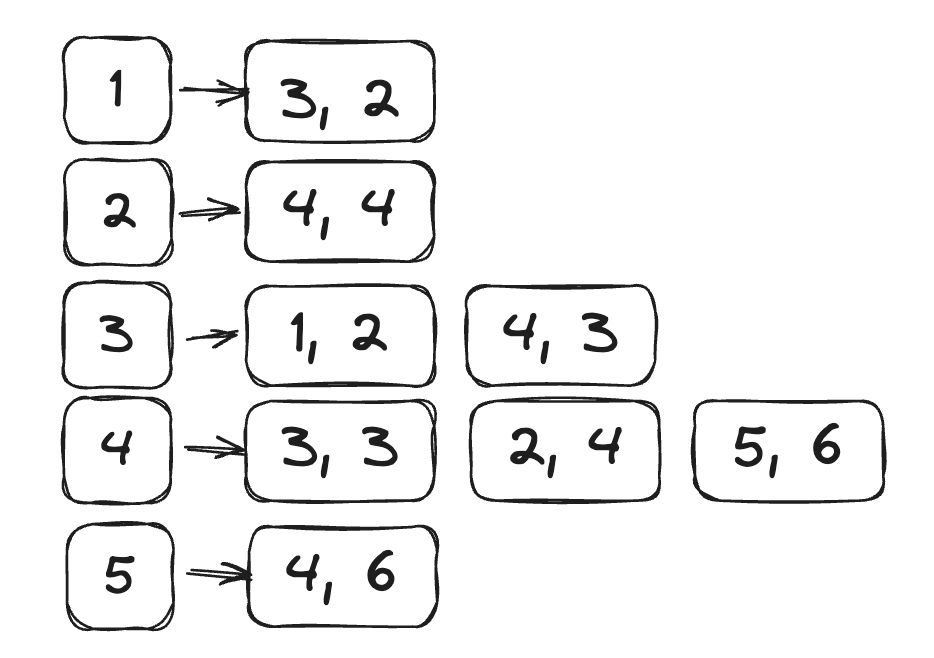
2. 임의의 노드에서 BFS 을 수행하고 탐색할 때 각 노드의 거리를 배열에 저장합니다. 일단 손으로 풀어볼 때는 동작 원리를 제대로 정의하기 위해서 노드 2에서 시작하는 것으로 하겠습니다.
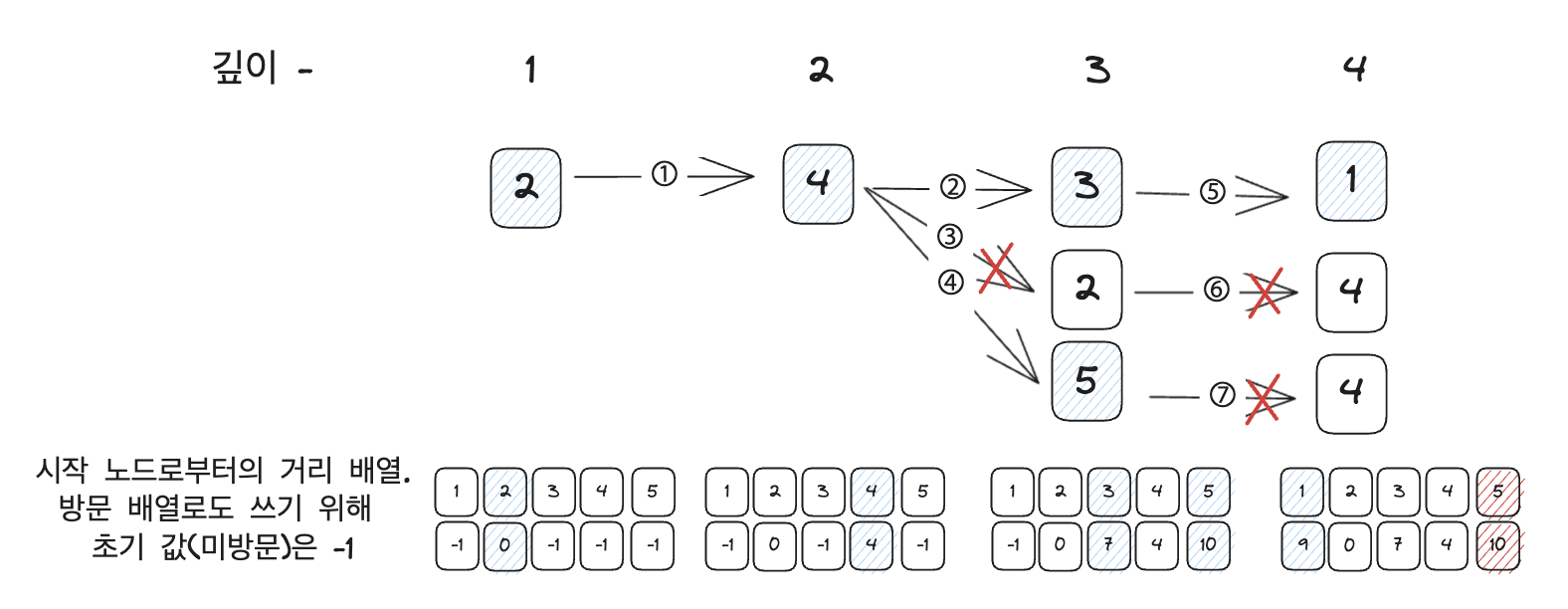
이렇게 탐색을 하고 나면 출발 노드 2 에서 가장 긴 경로가 노드 5로 갈 때라는 것을 알 수 있습니다.
즉, 노드 2 와 노드 5 중 하나의 노드 이상이 트리에서 가장 긴 경로의 시작점이라는 것을 알아냈습니다. 그렇다면 이제 노드 5에서 다시 가장 긴 경로를 찾으면 됩니다.
위와 똑같은 방법으로 BFS 탐색을 하면 노드 1로 갈 때 경로가 최대인 11 이라는 것을 알 수 있습니다. 이렇게 하면 문제의 요구사항을 맞출 수 있습니다.
3. 슈도코드
V: 노드 개수
graph: 그래프를 인접 리스트로
distance 배열: 시작 노드로부터 거리을 저장. 초기 값은 -1
graph 초기화.
queue : bfs 에 사용할 큐. LinkedList 로
// 임의의 노드에서 BFS 시작
tempDestNode = bfs(1) // 임의의 노드에서 가장 먼 노드 정보 저장
resultNode = bfs(tempDestNode.node)
sout(resultNode.weight)
// bfs method
bfs(startNode){
Node returnNode: 결과로 리턴할 가장 긴 경로의 노드와 그 거리
큐에 시작노드 넣기
시작 노드는 거리가 0.
큐가 빌 때까지 {
int curNode = queue.poll()
for(모든 adjNode 에 대해){
방문하지 않았으면 큐에 add
// 해당 노드까지의 거리 저장
시작 노드부터 curNode 까지의 거리인 distance[curNode] 값 + curNode 에서 adjNode 까지의 거리를 distance 에 저장
returnNode.weight = (기존 returnNode.weight 와 adjNode 까지의 거리 중 최대값 저장)
}
}
return returnNode;
}
class Node{
int node;
int weight'
}
4. 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class BaekJun1167Self {
static ArrayList<Edge>[] graph;
static int distance[];
static Queue qu;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int V = Integer.parseInt(br.readLine());
graph = new ArrayList[V + 1];
distance = new int[V + 1];
for (int i = 1; i <= V; i++) {
graph[i] = new ArrayList<>();
distance[i] = -1;
}
for (int i = 1; i <= V; i++) {
st = new StringTokenizer(br.readLine());
int tokenCnt = st.countTokens();
int node = Integer.parseInt(st.nextToken());
for (int j = 1; j < tokenCnt - 2; j = j + 2) {
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
graph[node].add(new Edge(a, b));
}
}
br.close();
qu = new LinkedList();
Edge startNode = new Edge(1, -1);
startNode = bfs(startNode);
for (int i = 1; i <= V; i++) {
distance[i] = -1;
}
Edge resultNode = bfs(startNode);
System.out.println(resultNode.weight);
}
static Edge bfs(Edge edge) {
qu.offer(edge);
distance[edge.node] = 0;
Edge returnNode = new Edge(1, -1);
while (!qu.isEmpty()) {
Edge curNode = (Edge) qu.poll();
for (Edge adjNode : graph[curNode.node]) {
if (distance[adjNode.node] == -1) {
qu.add(adjNode);
distance[adjNode.node] = distance[curNode.node] + adjNode.weight;
if (distance[adjNode.node] > returnNode.weight) {
returnNode.node = adjNode.node;
returnNode.weight = distance[adjNode.node];
}
}
}
}
return returnNode;
}
static class Edge {
int node;
int weight;
public Edge(int node, int weight) {
this.node = node;
this.weight = weight;
}
}
}
'Java > 코딩테스트' 카테고리의 다른 글
| 그리디(Greedy) 자바 백준 11047, 1715, 1744 (0) | 2023.07.20 |
|---|---|
| 이진 탐색 (Binary Search) 자바 백준 1920 2343 1300 (3) | 2023.07.19 |
| DFS(깊이 우선 탐색) 자바 백준 11724, 2023, 13023 (0) | 2023.07.17 |
| 버블 정렬 - 자바 백준 수 정렬하기: 2750, 버블 소트: 1377 (0) | 2023.06.01 |
| 자바 PriorityQueue (0) | 2023.05.29 |