정수론
수학에서 정수론은 수의 성질을 공부하는 분야입니다. 실제 코딩테스트에서는 정수론의 분야가 굉장히 방대하기 때문에 가장 많이 등장하는 소수, 오일러 피, 호제법에 관련하여 학습합니다.
소수
소수(prime number) 는 자신보다 작은 2개의 자연수를 곱해서 만들 수 없는 1보다 큰 자연수를 말합니다. 1과 자기 자신 외에 약수가 없는 수입니다.
소수를 구하는 대표적인 방법은 에라토스테네스의 체가 있습니다.
에라토스테네스의 체
1. 구하고자 하는 소수의 범위만큼 1차원 배열 생성.
2. 2부터 시작해서 현재 숫자가 지워지지 않았다면 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지웁니다. 처음으로 선택된 숫자는 지우지 않습니다.
3. 배열의 끝까지 2를 반복한 후에 배열에서 남아 있는 모든 수를 출력합니다.
1부터 31까지의 수 중 소수를 구하는 예시입니다.
1. 먼저 주어진 범위까지의 배열을 생성합니다. 1은 소수가 아니기 때문에 삭제하고, 2부터 시작합니다.

2. 선택한 수의 배수를 모두 삭제합니다.

3. 다음 지워지지 않은 수를 선택합니다. 선택한 수의 모든 배수를 삭제합니다. 이미 지운 수는 삭제하지 않습니다.

4. 앞의 과정을 끝까지 반복합니다.
5. 삭제되지 않은 수들이 해당 범위의 모든 소수입니다.

즉, {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31} 이 소수입니다.
에라토스테네스의 체의 시간 복잡도
일반적으로 에라토스테네스의 체를 사용하면 이중 for 문을 사용하여 시간 복잡도가 O(N²) 정도라고 판단할 수 있지만 실제 시간 복잡도는 O(Nlog(logN)) 입니다. 배수를 삭제하는 연산으로 실제 구현에서 바깥쪽 for 문을 생략하는 경우가 자주 일어나기 때문입니다. 그러므로 현제 소수를 구하는 문제에서 일반적으로 이 방법을 사용합니다.
백준 1929 소수 구하기
https://www.acmicpc.net/problem/1929
1929번: 소수 구하기
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
www.acmicpc.net
1. 문제 분석
N 의 최대 범위가 1,000,000 이므로 범위 내에 수마다 소수인지 판별하면 시간 초과가 날 것입니다. 에라토스테네스의 체를 이용해야 합니다.
2. 손으로 풀기
위에서 에라토스 테네스의 체 원리를 설명하는 부분에서의 풀이와 같습니다.
1. 먼저 크기가 N-1 인 배열을 선언하고 2 부터 N까지의 수로 채웁니다.
2. 숫자 2부터 N의 제곱근까지 값을 탐색합니다. 그 값의 배수는 0으로 바꿉니다.
3. 배열에 남아잇는 수 중에서 M 이상 N 이하의 수를 출력합니다.
왜 N 의 제곱근까지만 탐색하나요?
N 이 만약 a * b 이면 a 와 b 둘 중 한 수는 N의 제곱근보다 클 수 있지만 두 수 모두 N 의 제곱근보다 클 수는 없습니다. 따라서 N의 제곱근 까지만 확인해도 전체 범위의 소수를 판별할 수 잇습니다.
예를 들어서 25 라는 수가 있으면 25 = 5² 입니다. 따라서 5까지만 확인하고 소수 판별을 진행하면 됩니다.
3. 슈도코드
M: 시작 범위, N: 종료 범위
pN: 크기가 N+1 인 배열 0, 1, 2, 3, ... N
인덱스가 i 일 때 pn{i] = i
for(현재 수는 2부터 시작)
만약 현재수가 0 이 아니면
인덱스 를 현재수의 배수로 증가시켜 가면서
그에 해당하는 수를 배열에서 0으로 바꿈.
pN 의 M ~ N 사이이 모든 수를 탐색해가면서
0 이 아니면 출력한다.4. 코드
public class BaekJun1929Self {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int M = Integer.parseInt(st.nextToken());
int N = Integer.parseInt(st.nextToken());
int last = (int) (Math.sqrt(N));
int[] pN = new int[N + 1];
for (int i = 2; i <= N; i++) {
pN[i] = i;
}
for (int i = 2; i <= last; i++) {
int curNum = pN[i];
if (curNum != 0) {
int j = 2;
while (curNum * j <= N) {
pN[curNum * j] = 0;
j++;
}
}
}
for (int i = M; i <= N; i++) {
if (pN[i] != 0) {
System.out.println(pN[i]);
}
}
}
}
백준 1456 거의 소수
https://www.acmicpc.net/problem/1456
1456번: 거의 소수
어떤 수가 소수의 N제곱(N ≥ 2) 꼴일 때, 그 수를 거의 소수라고 한다. 두 정수 A와 B가 주어지면, A보다 크거나 같고, B보다 작거나 같은 거의 소수가 몇 개인지 출력한다.
www.acmicpc.net
1. 문제 분석
입력으로 받은 범위에서 모든 소수를 미리 구한 후에 이 소수들을 제곱해가면서 범위 내에 있는지를 체크하면 됩니다.
2. 손으로 풀기
1. 먼저 에라토스테네스의 체를 사용해서 범위 내에 모든 소수를 구합니다. 이 때 범위는 1부터 시작해서 B의 제곱근까지만 구하면 됩니다.
그 이유는 어차피 우리가 원하는 것은 소수의 N 제곱인 것들을 구하는 것이기 때문입니다. 예를 들어서 A 가 1 이고 B 가 121 일 때 11 이 121 의 제곱근입니다. 11² = 121 이고 12² = 144 인 것처럼 B의 제곱근보다 큰 수는 소수이더라도 제곱하면 항상 B 보다 클 수 밖에 없습니다.
2. 구한 소수에 대해서 가장 작은 수부터 시작해서 자기 자신의 수를 계속해서 곱해가면서 범위 내에 있는지를 판단하고 카운트하면 됩니다.
3. 슈도코드
A: 왼쪽 범위, B: 오른쪽 범위
ans = 0
pNA: 소수 판별 집합.
pNA을 인덱스와 같은 값으로 2 .. .루트(B) 초기화
pNL : 소수인 값만 저장할 리스트
for(2부터 루트(B) 까지 ){
if(현재 수가 0 이 아니다){
현재수를 리스트에 추가
배열에서 현재 수의 배수인 인덱스의 값은 모두 0 으로
}
}
for(pNL 의 모든 수에 대해){
j = 2
while( 현재수의 i 제곱한 수 x이 범위에 있으면 계속){
cnt++
j++
}
}
sout(cnt)
4. 코드
public class BaekJun1456Self {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
br.close();
long A = Long.parseLong(st.nextToken());
long B = Long.parseLong(st.nextToken());
int ans = 0;
int last = (int) Math.sqrt(B);
int[] pNA = new int[last + 1]; // 최대 10^7 크기
List<Integer> pNL = new ArrayList<>();
for (int i = 2; i <= last; i++) {
pNA[i] = i;
}
for (int i = 2; i <= last; i++) {
int curNum = pNA[i];
if (curNum != 0) {
int j = 2;
pNL.add(curNum);
while (i * j <= last) {
pNA[i * j] = 0;
j++;
}
}
}
for (double curNum : pNL) {
double temp = 1;
while (true) {
temp *= curNum;
if (curNum >= A / temp && curNum <= B / temp) {
ans++;
} else if (curNum > B / temp) {
break;
}
}
}
System.out.println(ans);
}
}
5. 틀렸던 코드
이 문제를 처음 풀 때 런타임에러(Arithmetic) 이 계속해서 발생해서 풀지 못했습니다.
먼저 틀렸던 코드는 아래와 같습니다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
long A = Long.parseLong(st.nextToken());
long B = Long.parseLong(st.nextToken());
long last = (long) Math.sqrt(B);
long[] pNA = new long[Math.toIntExact(B + 1)];
List<Long> pNL = new ArrayList<>();
int ans = 0;
for (long i = 2; i <= B; i++) {
pNA[Math.toIntExact(i)] = i;
}
for (long i = 2; i <= last; i++) {
long curNum = pNA[Math.toIntExact(i)];
if (curNum != 0) {
pNL.add(curNum);
long j = 2;
while (i * j <= B) {
pNA[Math.toIntExact(i * j)] = 0;
j++;
}
}
}
for (long curPN : pNL) {
long j = 2;
while (true) {
long curNum = (long) Math.pow(curPN, j);
if (curNum >= A && curNum <= B) {
ans++;
j++;
} else if (curNum > B) {
break;
} else { // curNum < A
j++;
}
}
}
System.out.println(ans);
}
먼저 자바에서 배열은 2³¹ - 1 = 2,147,483,647 개의 아이템만 가질 수 있습니다. 문제에서는 B 가 최대 10¹⁴ 이 될 수 있습니다. 그러므로 입력에 따라 문제가 생길 수 있습니다.
또한 curNum 이 매우 커질 것을 대비해서 long 타입으로 선언했지만 long 타입의 범위도 넘어설 수 있습니다. 그러므로 이 방식 또한 적합하지 않습니다.
거의 소수인지를 판별하는 조건에서 (curPN)ᴺ >= A && (curPN)ᴺ <= B 인 식을 생각을 조금 바꾸어서
curPN >= A/(curPN)ᴺ⁻1 && curPN <= B/(curPN)ᴺ⁻¹ 의 형태로 바꾸어야 했습니다.
백준 1747 소수&팰린드롬
https://www.acmicpc.net/problem/1747
1747번: 소수&팰린드롬
어떤 수와 그 수의 숫자 순서를 뒤집은 수가 일치하는 수를 팰린드롬이라 부른다. 예를 들어 79,197과 324,423 등이 팰린드롬 수이다. 어떤 수 N (1 ≤ N ≤ 1,000,000)이 주어졌을 때, N보다 크거나 같고,
www.acmicpc.net
1. 문제 분석
에라토스테네스의 체를 이용해서 최대 범위에 해당하는 모든 소수를 구하는 것과, 이 소수가 N 보다 크거나 같으면서 팰린드롬 수인지를 판별하는 문제 입니다. 크게 어려울 것 없이 위에 있는 문제들과 매우 비슷합니다.
문제와 입력 조건에서 입력한 수 N은 최대 1,000,000 이고 N 보다 크거나 소수이면서 팰린드롬인 수 중 가장 작은 수를 구하라고 했습니다. 즉, 이 문제에서는 N 이 1,000,000 일 때 출력되는 정답(availableMax 라고 하겠습니다.) 이하로는 소수인지 판별할 필요가 없습니다.
먼저 탐색 범위를 줄이기 위해 availableMax 을 따로 구하고 이 범위에 대해서 로직을 만들어 나가겠습니다.
2. 손으로 풀기
바로 위 1. 문제분석에서 말했듯 먼저 availableMax 을 구하는 과정부터 설명하겠습니다.
1. 먼저 10,000,000 이하인 모든 소수를 구합니다.
availableMax 가 정확히 몇인지는 모르지만 아마 10,000,000 보다는 작을 것을 예상하고 구하는 것입니다.

2. 각 소수에 대해서 팰린드롬 수인지를 판별합니다. 이 때 투 포인터를 이용하면 됩니다.
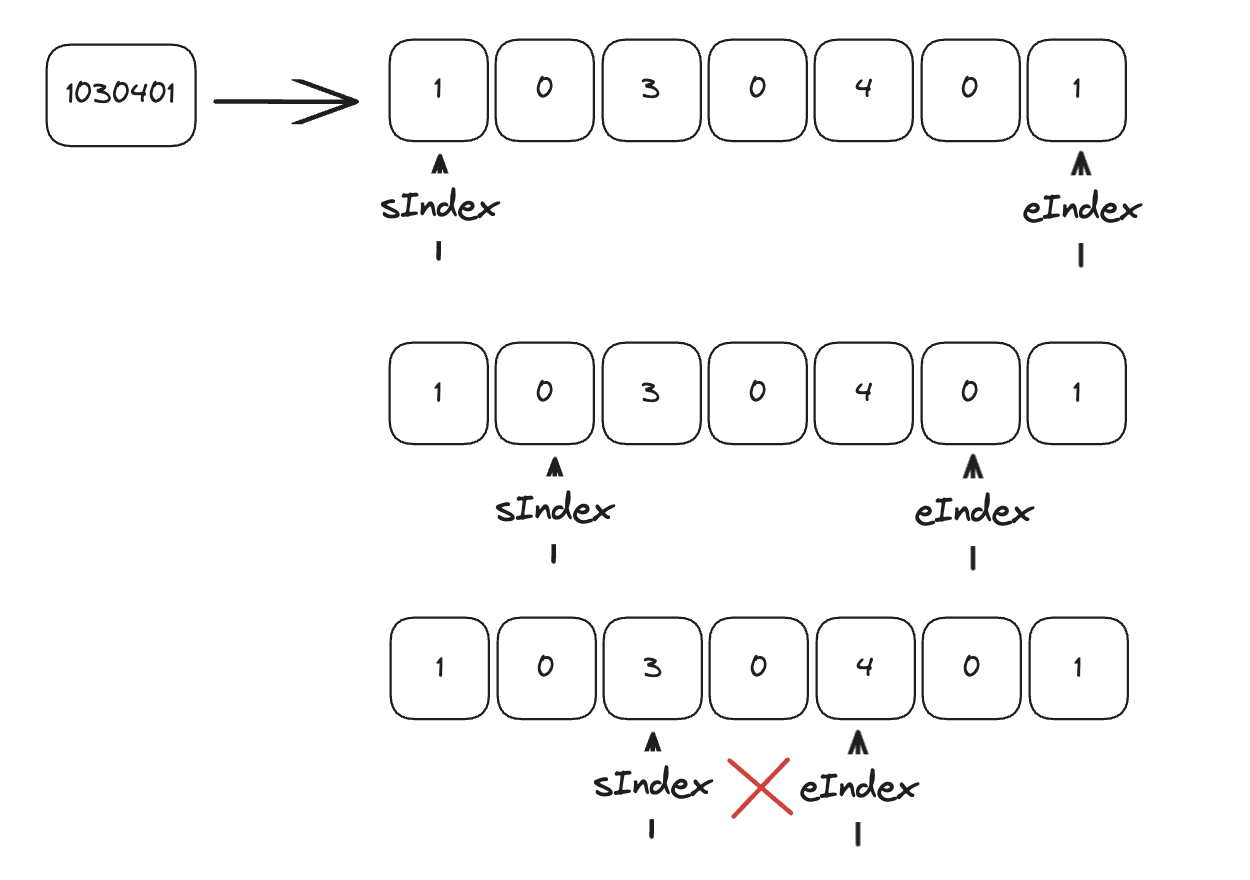
위 그림처럼 앞 뒤 숫자를 비교해가면서 같으면 인덱스를 이동시킵니다. 이 때 sIndex >= eIndex 이면 팰린드롬 수이게 됩니다.
그렇게 1부터 10,000,000 사이에 있는 모든 소수이면서 팰린드롬 수를 알아냈습니다.
[2, 3, 5, 7, 11, 101, 101, 131, 131, 151, 151, 181, 181, 191, 191, 313, 313, 353, 353, 373, 373, 383, 383, 727, 72 ... 98689, 98689, 1003001, 1003001, 1008001, ... 98689, 98689, 1003001, 1003001, 1008001,]
이제 이 1,003,001 보다 작거나 같은 수들에 대해서만 소수인지, N보다 크거나 같은 수인지, 팰린드롬 수인지 판별하면 됩니다
만약 2부터 10,000,000 까지 소수를 출력하고자 했는데 문제가 생김. 2431 보다 앞의 수들은 출력되지 않는다면?

IntelliJ 기준으로는 이 링크를 참고하여 IDE 을 수정하면 됩니다. https://happy-jjang-a.tistory.com/22 <- 해결
3. availableMax 을 알아내기 위한 코드
public class BaekJun1747 {
public static void main(String[] args) throws IOException {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int[] exPN = new int[10_000_000];
int last = (int) Math.sqrt(10_000_000);
List<Integer> pNList = new ArrayList<>();
for (int i = 2; i < exPN.length; i++) {
exPN[i] = i;
}
for (int i = 2; i <= last; i++) {
int cur = exPN[i];
if (cur != 0) {
int j = 2;
while (cur * j < 10_000_000) {
exPN[cur * j] = 0;
j++;
}
}
}
for (int i = 2; i < 10_000_000; i++) {
int curNum = exPN[i];
if (curNum != 0) {
char[] curC = String.valueOf(curNum).toCharArray();
int sIndex = 0;
int eIndex = curC.length - 1;
while (sIndex <= eIndex) {
if (curC[sIndex] == curC[eIndex]) {
sIndex++;
eIndex--;
if (sIndex >= eIndex) {
pNList.add(curNum);
}
} else {
break;
}
}
}
}
bw.write(pNList.toString());
bw.flush();
bw.close();
}
}결과
[2, 3, 5, 7, 11, 101, 101, 131, 131, 151, 151, 181, 181, 191, 191, 313, 313, 353, 353, 373, 373, 383, 383, 727, 72 ... 98689, 98689, 1003001, 1003001, 1008001, ... 98689, 98689, 1003001, 1003001, 1008001,]
4. 정답 코드
public class BaekJun1747 {
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int maxAvailable = 1_003_001;
int[] exPN = new int[1_003_002];
boolean isEnd = false;
for (int i = 2; i <= maxAvailable; i++) {
exPN[i] = i;
}
for (int i = 2; i <= maxAvailable; i++) {
if (!isEnd) {
int curNum = exPN[i];
if (curNum != 0) {
int j = 2;
while (curNum * j <= maxAvailable) {
exPN[curNum * j] = 0;
j++;
}
if (curNum >= N) {
char[] curC = String.valueOf(curNum).toCharArray();
int sIndex = 0;
int eIndex = curC.length - 1;
while (sIndex <= eIndex) {
if (curC[sIndex] == curC[eIndex]) {
sIndex++;
eIndex--;
if (sIndex >= eIndex) {
System.out.println(curNum);
isEnd = true;
break;
}
} else {
break;
}
}
}
}
}
}
}
}
백준 1016 제곱 ㄴㄴ 수
1016번: 제곱 ㄴㄴ 수
어떤 정수 X가 1보다 큰 제곱수로 나누어 떨어지지 않을 때, 그 수를 제곱ㄴㄴ수라고 한다. 제곱수는 정수의 제곱이다. min과 max가 주어지면, min보다 크거나 같고, max보다 작거나 같은 제곱ㄴㄴ수
www.acmicpc.net
1. 문제 분석
min의 최대값이 1,000,000,000,000 이어서 시간 복잡도가 매우 클 것 같지만 실제로는 min, max 사이의 수를 구하는 것이므로 1,000,000 의 범위가 되어 시간 내에 충분히 해결 가능합니다.
이 문제도 이전 문제들에서 적용했던 에라토스테네스의 체를 이용하며 여러 방법을 결합해서 문제를 풀면 됩니다. 조금 복잡해보일 수도 있습니다.
2. 손으로 풀기
제곱 ㄴㄴ 수는 1보다 큰 자연수의 제곱으로 나누어 떨어지면 안됩니다. 문제 조건에서 가능한 max 값은 1,000,001,000,000 인데
먼저 어떤 수 x 가 4² 으로 나누어 떨어진다면 이 수는 제곱 ㄴㄴ 수가 아니게 됩니다. 그런데 x 는 4² 로 나누어 떨어지기 이전에 2² 로 나누어 떨어집니다. 마찬가지로 어떤 수 y 가 9² 로 나누어 떨어진다면 그 이전에 y 는 3² 로 나누어 떨어집니다. 즉, 제곱 ㄴㄴ 수는 소수의 제곱으로 나누어 떨어지지 않는 수가 됩니다.
그러면 수를 소수의 제곱으로 나눌 때 어떤 범위의 소수로 지정해야 할까요? 만약 max 값이 150 이라고 할 때 150보다 작거나 같은 자연수의 제곱수는 144 = 12² 입니다.
즉, 2 부터 (int) Math.sqrt(max) 값까지의 소수 범위가 됩니다. last = (int) Math.sqrt(max) 라고 하겠습니다.
그리고 입력이 11 150 이라고 생각하고 문제를 풀어보겠습니다.
1. 에라토스테네스의 체를 이용하여 2 ~ 12(=last) 범위 내에 모든 소수를 구한다.
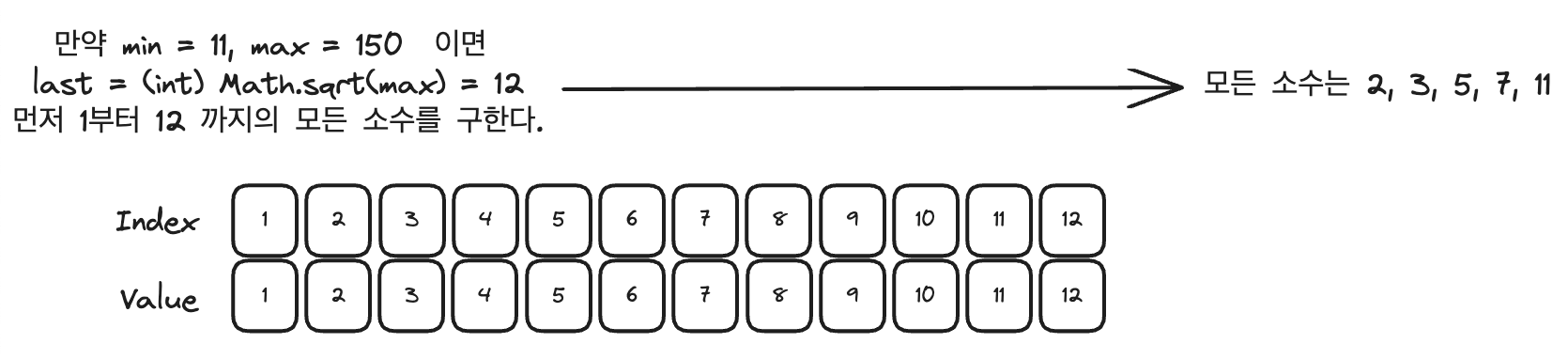
2. min 값부터 max 까지의 값을 담는 배열 numArr 을 생성한다.

3. 소수에 대해 numArr 에 있는 (소수)² 의 배수인 값들을 모두 0 으로 만든다. 그리고 이 과정을 모든 소수에 대해서 반복한다.
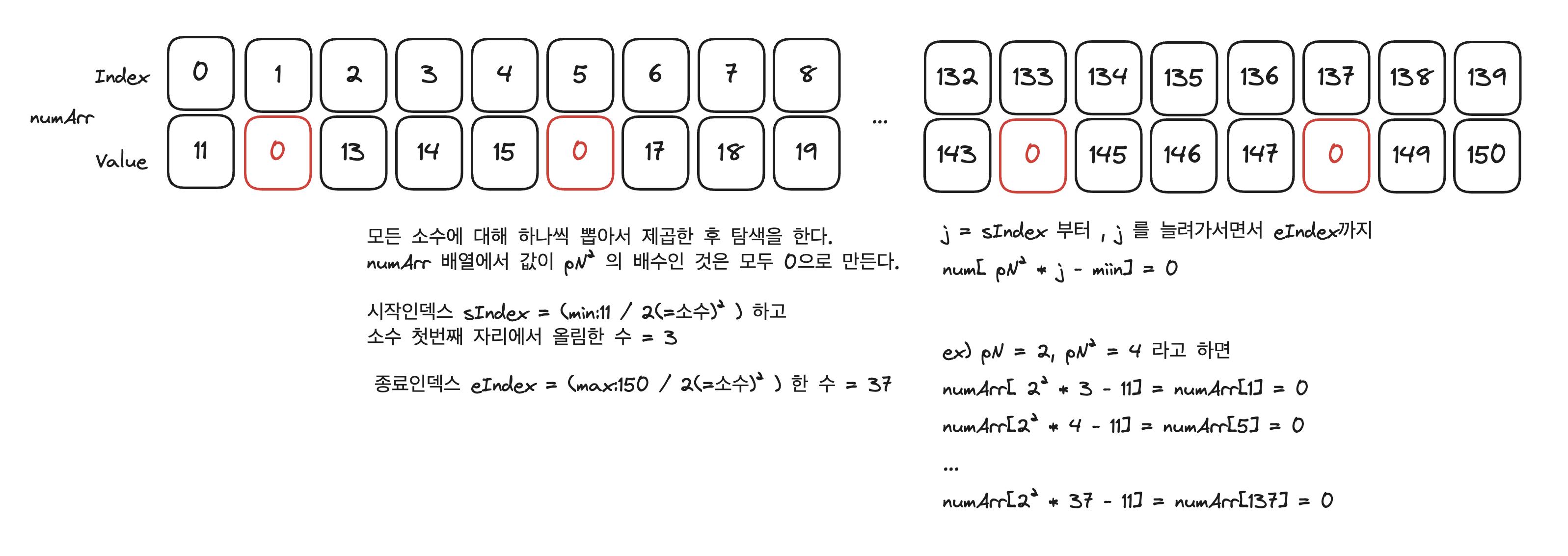
4. 3의 과정을 모든 소수에 대해 반복 완료 했다면 numArr 에 있는 0 이 아닌 수를 모두 센 후 출력한다.
3. 코드
public class BaekJun1016 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
long min = Long.parseLong(st.nextToken()); // 11
long max = Long.parseLong(st.nextToken()); // 150
int numCnt = (int) (max - min + 1); // 150 - 11 + 1 = 140
int last = (int) Math.sqrt(max);
int[] pNArr = new int[last + 1];
List<Integer> pNL = new ArrayList<>();
long[] numArr = new long[numCnt];
for (int i = 2; i <= last; i++) {
pNArr[i] = i;
}
for (int i = 2; i <= last; i++) {
int cur = pNArr[i];
if (cur != 0) {
pNL.add(cur);
int j = 2;
while (i * j <= last) {
pNArr[i * j] = 0;
j++;
}
}
}
for (int i = 0; i < numCnt; i++) {
numArr[i] = min + i;
}
for (long pNum : pNL) {
long pNum_2 = pNum * pNum;
long sIndex = min / (pNum_2);
long eIndex = max / (pNum_2);
if (min % (pNum_2) > 0) {
sIndex++;
}
for (long i = sIndex; i <= eIndex; i++) {
int index = (int) (pNum * pNum * i - min);
numArr[index] = 0;
}
}
int res = 0;
for (int i = 0; i < numCnt; i++) {
if (numArr[i] != 0) {
res++;
}
}
System.out.println(res);
}
}이 경우 시간은 284 ms 가 나왔습니다.
4. 다른 정답 코드
public class BaekJun1016 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
long min = Long.parseLong(st.nextToken());
long max = Long.parseLong(st.nextToken());
int numCnt = (int) (max - min + 1);
int last = (int) Math.sqrt(max);
// 최대값과 최소값의 차이만큼 배열 선언
boolean[] check = new boolean[numCnt];
// 2의 제곱 수인 4 부터 Max 보다 작거나 같은 값까지 반복
for (long i = 2; i <= last; i++) {
long pow = i * i;
long sIndex = min / pow;
if (min % pow != 0) {
sIndex++; // 나머지가 있다면 1을 더해야 min 보다 큰 제곱수에서 시작됨.
}
for (long j = sIndex; pow * j <= max; j++) {
check[(int) ((j * pow) - min)] = true; // 제곱수를 true 로
}
}
int cnt = 0;
for (int i = 0; i < numCnt; i++) {
if (!check[i]) {
cnt++;
}
}
System.out.println(cnt);
}
}이 정답 코드에서는 따로 소수를 구한 후에 소수의 제곱에 대해서 수들이 나누어 떨어지는지를 구하지 않고, 2부터 시작하는 모든 자연수의 제곱에 대해 나누어 떨어지는지를 구합니다. 시간초는 176ms 이 나왔습니다.
당연히 모든 수에 대해 제곱해서 나누어 떨어지는 것보다 범위에 해당하는 소수만 구하고 그 소수에 대해서만 제곱해서 나누어 떨어지는지를 구하는 것이 시간이 덜 걸릴 것이라고 생각했는데 그렇지 않았네요..
물론 3번 코드를 더 최적화해서 시간을 줄일 수도 있습니다. 그런데 최적화한 코드도 252 ms 가 나온 것으로 봐서 2이상의 모든 자연수의 제곱으로 구하는 것이 더 시간이 덜 걸렸네요
제가 알기로는 시간초를 재는 것은 백준에서 제공하는 모든 테스트 케이스를 통과하는 시간을 기준으로 하는 것이기 때문에 절대적인 지표는 아니지만 소수를 구하기 위해서 반복문을 한번 더 도는 것이 오히려 시간이 더 드는 게 맞는 것 같네요.
'Java > 코딩테스트' 카테고리의 다른 글
| 유클리드 호제법 -1 자바 백준 BOJ 1934 1850 (0) | 2023.07.25 |
|---|---|
| 오일러 피 자바 백준 BOJ 11689 (0) | 2023.07.25 |
| 그리디(Greedy) 자바 백준 1931, 1541 (0) | 2023.07.21 |
| 그리디(Greedy) 자바 백준 11047, 1715, 1744 (0) | 2023.07.20 |
| 이진 탐색 (Binary Search) 자바 백준 1920 2343 1300 (3) | 2023.07.19 |