오일러 피
오일러 피 함수 P[N]는 1부터 N까지 범위의 N과 서로소인 자연수의 개수를 뜻합니다. 실제 오일러 피 함수는 증명과정을 공부해야 완벽히 알 수 있지만 이 포스팅에서는 코딩 테스트에 사용하기 위한 구현 부분만 알아봅니다.
오일러 피 함수의 원리는 에라토스테네스의 체와 비슷합니다.
오일러 피 함수의 원리
1. 구하고자 하는 오일러 피의 범위만큼 배열 초기화
2. 2부터 시작해서 소수일 때(현재 배열의 값과 인덱스가 같으면) 현재 선택된 숫자[K] 의 배수에 해당하는 수를 배열에 끝까지 탐색하며 P[i] = P[i] - P[i]/K 연산을 수행. 이 때 i 는 K의 배수.
3. 배열의 끝까지 2번 과정을 반복하여 오일러 피 함수를 완성.
그림과 예시와 함께 더 자세히 알아봅시다.
1. 구하고자 하는 범위 15 까지 배열을 생성한 후 2를 선택
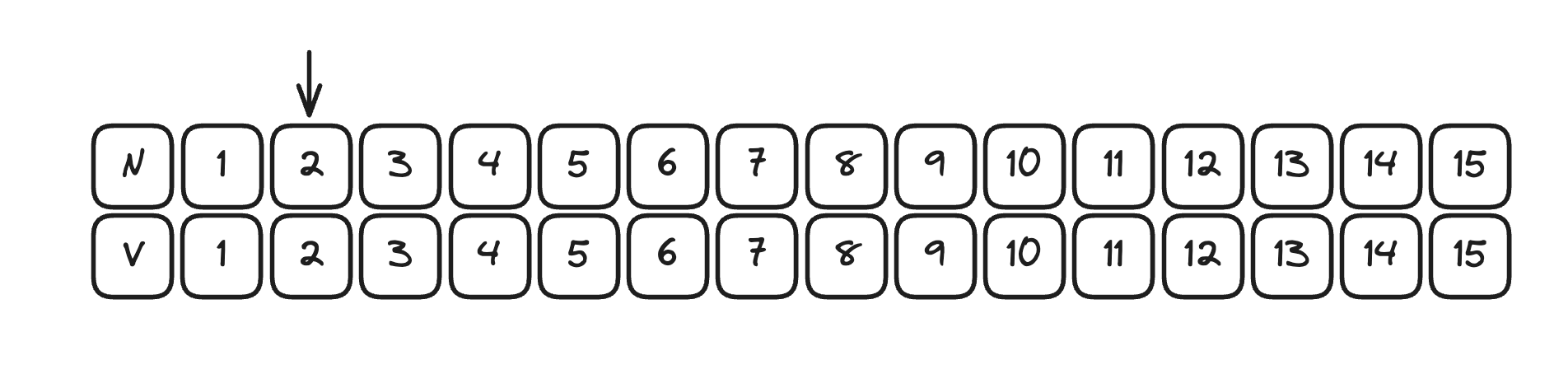
2. 2의 모든 배수마다 P[i] = P[i] - P[i]/2 연산을 수행해서 값을 갱신. (ex. 4 = 8 - 8/2). 이렇게 소수 구하기에서 배수를 지우는 부분만 P[i] = P[i] - P[i]/K 로변경하면 오일러 피 함수를 간단히 구현할 수 있음.

3. 탐색을 계속 진핸하면서 N = V (소수인 곳)을 찾아 값을 갱신. 배열이 끝날 때까지 이 과정을 반복합니다.

과정을 마무리했을 때 1 과 15 사이에서 15와 서로소가 되는 수의 개수는 8개입니다. (1, 2, 4, 7, 8, 11, 13, 14)
오일러 피 함수 수학으로 이해
12에 대한 오일러 피 함수를 구하는 경우를 생각해봅시다.
초기 상태 -> N(12) = 12: 서로소가 될 수 있는 후보 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
2의 배수로 인한 후보 탈락 -> N(12) = 12 - (12 / 2) = 6 : {1, 3, 5, 7, 9, 11}
3의 배수로 인한 후보 탈락 -> N(12) = 6 - (6 / 3) = 4: {1, 5, 7, 11}
1부터 12 사이에 있는 다른 소수들은 12의 약수가 아니므로 N(12) 에 영향을 미치지 않습니다.
그러므로 N(12) = 4입니다. 1과 12 사이에서 12와 서로소가 될 수 있는 자연수의 개수는 {1, 5, 7, 11} 로 4개라는 의미입니다.
오일러 피를 구하는 문제는 자주 출제되지는 않지만 원리를 모르면 문제 접근 자체가 쉽지 않으니 정리해둡시다.
백준 11689 GCD(n, k) = 1
https://www.acmicpc.net/problem/11689
11689번: GCD(n, k) = 1
자연수 n이 주어졌을 때, GCD(n, k) = 1을 만족하는 자연수 1 ≤ k ≤ n 의 개수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
1. 문제 분석
GCD(n, k) = 1 이라는 것은 n 과 k 의 최대 공약수가 1이라는 것입니다. 즉, GCD(n,k)=1 을 만족하는 자연수의 개수가 오일러 피 함수 그 자체입니다. 이 경우 입력으로 받는 자연수 n 에 대해서만 오일러 피 함수값을 구하는 것이므로 1 부터 n 까지의 배열을 만들 필요는 없습니다. 또한 n은 최대 10¹² 이므로 이 크기의 배열을 만들 수도 없습니다.
2. 손으로 풀기
1. 먼저 결과값을 입력과 같게 둡니다. 예제 입력 4 처럼 n = 45 이면 res = 45 입니다.
2. 오일러 피의 원리처럼 2부터 루트(n) 까지 소인수인 경우 res 값과 n 값을 갱신합니다. res = res - (res / 소인수) 연산을 하고 n 에서 이 소인수는 나누기 연산으로 삭제합니다.
a. n = 45, 현재수 curN = 2 -> n % curN != 0 -> 소인수 아님.
b. curN = 3 -> n % curN == 0 -> 소인수임. res 와 n 값을 갱신
res = res - (res / curN). 즉, res = 45 - (45 / 3) = 30.
n 을 더 나누어 떨어지지 않을 때 까지 curN 으로 나누기. n = 45 / 3² = 5
45의 소인수 중에서 3을 약수로 갖는 모든 수를 지우는 역할을 합니다.
결과인 5는 45에서 3의 제곱 형태의 약수들을 모두 제거한 약수입니다.
c. (curN = 4) > (루트(n) = 루트(5)) . 이 부등식이 만족한다는 것은 현재 수보다 크거나 같은 수 중에서 소인수가 없다는 의미입니다. 그러므로 반복문을 종료합니다.
더 구체적으로 설명하면 만약 curN = 5, n = 77 인 상태라고 합시다. curN < 루트(n) 인 상태이죠. 이 경우에는 아직 소인수가 남아 있기 때문에 curN 을 늘려가면서 더 탐색해야 합니다. 혹은 curN = 5, n = 25 인 경우 curN == 루트(n) 입니다. 이 경우에도 소인수가 남아있죠. 당연히 이 경우는 n 이 curN² 입니다.
d. 반복문을 종료한 후에 현재 n 이 1보다 크면 해당 n 이 마지막 소인수라는 의미입니다. n = 5 입니다. res = res - (res / n) 연산으로 res 값을 마지막으로 업데이트한 후 출력합니다.
res = 30 - (30 / 5) = 24
3. 슈도코드
n: 소인수의 곱을 표현, 입력부터, res: 결과(처음에는 n)
for( 2 ~ 루트(n)까지){
if(현재수 curN 이 n의 소인수이면){
결과값 res = res - (res/curN)
n 에서 나누어 떨어지지 않을 때까지 소인수인 curN 으로 나눈 값으로 n 을 갱신.
}
}
if( n > 1){ // n 이 마지막 소인수일때
res = res - (res / n)
}
res 출력
4. 코드
public class BaekJun11689 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long n = Long.parseLong(br.readLine());
int last = (int) Math.sqrt(n);
long res = n;
for (int i = 2; i <= last; i++) {
if (n % i == 0) {
res = res - (res / i);
while (n % i == 0) {
n = n / i;
}
}
if ( i > (int) Math.sqrt(n)) break;
}
if (n > 1) {
res = res - (res / n);
}
System.out.println(res);
}
}'Java > 코딩테스트' 카테고리의 다른 글
| 유클리드 호제법 -2 자바 백준 BOJ 1033 칵테일 (0) | 2023.07.26 |
|---|---|
| 유클리드 호제법 -1 자바 백준 BOJ 1934 1850 (0) | 2023.07.25 |
| 정수론 소수 구하기 자바 백준 BOJ 1929 1456 1747 1016 (0) | 2023.07.24 |
| 그리디(Greedy) 자바 백준 1931, 1541 (0) | 2023.07.21 |
| 그리디(Greedy) 자바 백준 11047, 1715, 1744 (0) | 2023.07.20 |