sh1mj1_log

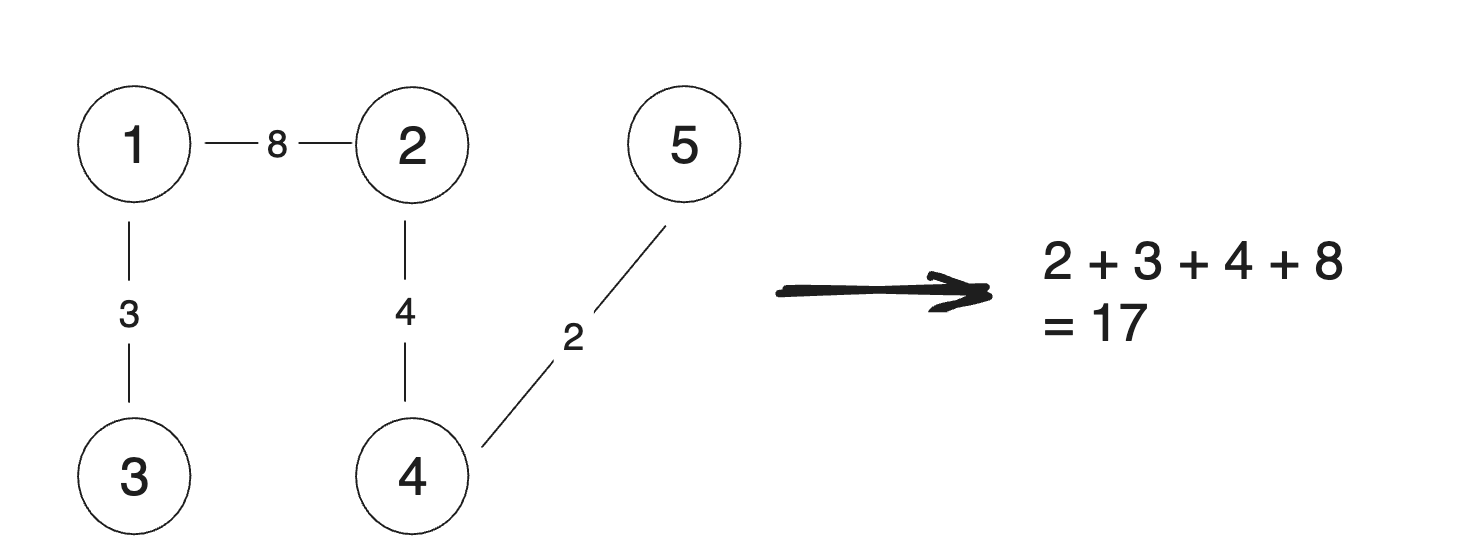
트리(Tree) 는 노드와 에지로 연결된 그래프의 특수한 형태입니다. 순한 구조(cycle) 이 없고, 1개의 루트 노드가 존재. 루트 노드를 제외한 노드는 단, 1개의 부모 노드를 가짐. 트리의 부분 트리(subtree) 역시 트리의 모든 특징을 따름. 리프노드는 트리에서 가장 하위에 존재하는 노드(자식 노드가 없는 노드) 입니다. 백준 11725 트리의 부모 찾기 https://www.acmicpc.net/problem/11725 11725번: 트리의 부모 찾기 루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오. www.acmicpc.net 1. 문제 분석 주어지는 데이터가 단순히 연결되어 있는 두 노드를 알려 주는 것이므로 데이터 ..

최소신장 트리 최소 신장 트리(Maximum Spanning Tree, MST)란 그래프에서 모든 노드를 연결할 때 사용된 에지들의 가중치의 합을 최소로 하는 트리입니다. 아래 특징을 가집니다. 사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않음. N 개의 노드가 있으면 최소 신장 트리를 구성하는 에지의 개수는 항상 N-1 개임. 최소 신장 트리 핵심 이론 1. 그래프 구현(에지 리스트), 유니온 파인드 배열 초기화 최소 신장 트리는 데이터를 노드가 아니라 에지를 중심으로 저장합니다. 그래서 벨만-포드 알고리즘에서처럼 에지 리스트의 형태로 저장해야 합니다. Edge 클래스는 일반적으로 노드 변수 2개, 가중치 변수 1개로 구성됩니다. 사이클 처리를 위한 유니온 파인드 배열도 초..

플로이드-워셜(Floyd-warshall) 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 주요 특징은 아래와 같습니다. 기능 특징 시간 복잡도 (V: 노드 수) 모든 노드 간에 최단 경로 탐색 ▪️ 음수 가중치 에지가 있어도 수행할 수 있음. ▪️ 동적 계획법의 원리를 이용해서 알고리즘에 접근 O(V³) 플로이드-워셜의 핵심 이론 플로이드-워셜 알고리즘을 도출하는 가장 핵심적인 원리는 A 노드에서 B 노드까지의 최단 경로 'X'를 구했다고 가정했을 때 그 최단 경로 'X' 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로라는 것입니다. 위에 빨간색 경로가 노드 1 에서 노드 5로 가는 최단경로라고 합시다. 그렇다면 1 -> 4 최단 경로와 4 -> 5 의 최단 경로도 빨간색 경..

벨만-포드(bellman-ford moore) 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘입니다. 기능 특징 시간 복잡도 (V: 노드 수, E: 에지 수) 특정 출발 노드에서 다른 모든 노드까지의 최단 경로 탐색 - 음수 가중치 에지가 있어도 수행할 수 있음. - 전체 그래프에서 음수 사이클의 존재 여부를 판단할 수 있음. O(VE) 벨만 - 포드의 핵심 이론 아래 3가지 단계로 동작합니다. 1. 에지 리스트로 그래프를 구현하고 최단 경로 배열 초기화. 벨만-포드 알고리즘은 에지를 중심으로 동작하여 에지 리스트로 구현합니다. 다익스트라와 똑같이 출발 노드는 0, 다른 노드들은 ∞ 로 초기화합니다. 아래 그래프의 예에서 출발 노드는 1로 하여 벨만-포드 알고리즘을 진행해보겠습니다. 2. 모든 에지를 ..

다익스트라(dijkstra) 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 주요 특징은 아래와 같습니다. 기능 특징 시간 복잡도 (V: 노드 수, E: 에지 수) 출발 노드와 모든 노드 간의 최단 거리 탐색 에지는 모두 양수여야 함. O(ElogV) 다익스트라 최단 경로 알고리즘은 기본적으로 '그리디 알고리즘'으로 분류됩니다. 매번 '가장 비용이 적은 노드'를 선택해서 임의의 과정을 반복하기 때문입니다. 다익스트라 알고리즘 핵심 이론 아래 5 단계로 설명됩니다. 1. 인접 리스트로 그래프 구현 그래프가 위와 같을 때 인접리스트가 표현됩니다. 물론 그래프를 인접 행렬로 구현해도 좋지만 시간 복잡도 측면, N 의 크기가 클 것을 대비해서 보통 인접 리스트로 구현됩니다. 2. 최단 거리 배열 초기화 ..

위상정렬(topology sort)은 사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘입니다. 기능 특징 시간 복잡도(V: 노드 수, E: 에지 수) 노드 간의 순서를 결정함. 사이클이 없어야 함. O(V+E) 위상 정렬에서는 항상 유일한 값으로 정렬되지 않습니다. 또 사이클이 존재하면 노드 간의 순서를 명확히 정의할 수 없어 위상정렬을 적용할 수 없습니다. 아래 구체적인 시나리오를 통해서 단계별로 알아봅시다. 위상 정렬의 원리 1. 그래프에서 진입차수(in-degree) 을 저장합니다. 진입차수는 자기 자신을 가리키는 에지의 개수입니다. 1 에서 2, 3 을 가리키고 있으므로 D[2], D[3] 을 각각 1을 증가하는 식으로 계산하면 진입 차수 배열 D[N] 을 구할 수 있습니다. 2. 진입 차..

유니온 파인드 union-find 는 일반적으로 여러 노드가 있을 때 특정 2개의 노드를 연결해서 1개의 집합으로 묶는 union 연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성되어 있는 알고리즘입니다. union 연산 각 노드가 속한 집합을 1개로 합치는 연산입니다. 노드 a, b 가 a ∈ A, b ∈ B 이 때 union(a,b) 는 A ∪ B 을 뜻합니다. find 연산 특정 노드 a 에 관해 a 가 속한 집합의 대표 노드를 반환하는 연산입니다. 노드 a 가 a ∈ A 일 때 find(a) 는 A 집합의 대표 노드를 반환합니다. 유니온 파인드 알고리즘 구현 방법 유니온 파인드 알고리즘 구현 방법을 아래 예를 통해서 알아봅시다. 1. 유니온 파인드는 일반적으로 1차원 배..

https://sh1mj1-log.tistory.com/140 이전 글에서 계속 됩니다. 백준 1707 이분 그래프 https://www.acmicpc.net/problem/1707 1707번: 이분 그래프 입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 www.acmicpc.net 1. 문제 분석 노드를 집합 2개로 나눌 때 인접한 노드끼리 같은 집합이 되면 안 됩니다. 즉, 같은 위 그림처럼 인접해있으면 색이 달라야 한다는 의미입니다. 만약 사이클이 발생한다면 이분 그래프가 불가능합니다. 이런 경우를 어떻게 알아낼 수 있을까요? 탐색 매커니즘에서 탐색한 노드..

그래프는 3가지 구현 방법이 있습니다. 에지 리스트, 인접행렬, 인접 리스트 로 구현할 수 있습니다. 에지 리스트(Edge list) 에지를 중심으로 그래프를 표현합니다. 에지 리스트는 배열에 출발 노드, 도착 노드를 저장하여 에지를 표현합니다. 또는 출발 노드, 도착 노드, 가중치를 저장하여 가중치가 있는 에지를 표현합니다. 가중치 없는 그래프를 에지 리스트로 표현 가중치가 없는 그래프는 출발 노드와 도착 노드만 표현하므로 배열의 행은 2개면 충분합니다. 1에서 2로 뻗어나가는 에지는 [1,2] 로 표현합니다. 이처럼 방향이 있는 그래프는 순서에 맞게 노드를 배열에 저장하는 방식으로 포현합니다. 노드를 배열에 저장하여 에지를 표현하므로 에지 리스트라고 합니다. 가중치 그래프를 에지 리스트로 표현 가중치..

확장 유클리드 호제법 유클리드 호제법의 목적이 두 수의 최대 공약수를 구하는 것이라면 확장 유클리드 호제법의 목적은 방정식의 해를 구하는 것입니다. 제대로 이것을 이해하려면 수학적인 증명이 필요하지만 우리는 관련 알고리즘 구현만 알아봅시다. 확장 유클리드 호제법의 원리 해를 구하고자 하는 방정식은 ax + by = c 입니다. (a, b, c, x, y 는 정수) 위 방정식은 c % gcd(a,b) = 0 인 경우에만 정수해를 가집니다. 즉, c 가 a 와 b 의 최대 공약수의 배수인 경우에만 정수해를 가집니다. ax + by = c 가 정수해를 갖게 하는 c 의 최소값이 gcd(a,b) 라는 것을 의미합니다. 5x + 9y = 2 일 때 이 식을 만족하는 정수 x, y 을 구하는 과정을 봅시다. 1. ..